A) An adjacency matrix has as many rows and columns as there are nodes. The entries in an adjacency matrix are 0's and 1's. If there is an edge from node N to node M (in other words, if N and M are neighbors), then there is a 1 in row N, column M of the adjacency matrix. Note that in the situation we are considering, an edge from N to M is also an edge from M to N, so there will also be a 1 in row M, column N of the adjacency matrix. (In other words, the adjacency matrix will be symmetric across the main diagonal.)

For example, for this small client-server network:

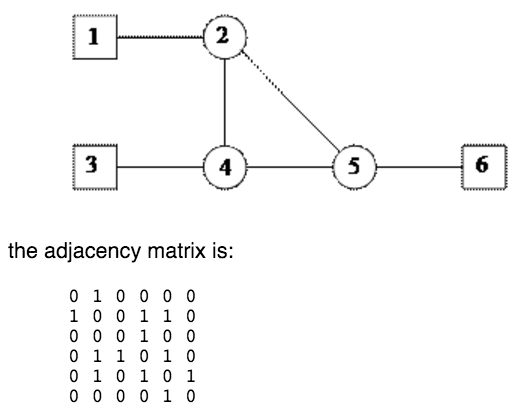
So, from the first row we can see th?at node 1is connected to node 2; the second row indicates that node 2 is connected to nodes 1, 4, and 5; the third row indicates that node 3 is connected to node 2, etc.

B) The solveClientServer function

The solveClientServer function takes one parameter, adjMatrix (an adjacency matrix), solves the linear system for a network of clients and servers represented by the adjacency matrix, and returns the results (i.e., the solution to the linear system) as a column vector. The solveClientServer function should assume that the adjacency matrix is valid.

Recall that the equations for this linear system are

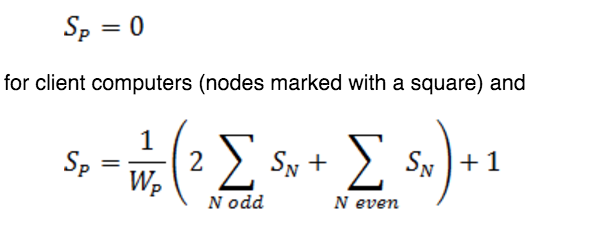
for servers (nodes marked with a circle), where the first sum is over all odd-numbered nodes that are linked to node P, the second sum is over all the even-numbered nodes that are linked to node P, and the value of W_P is a weighted sum of the number of nodes that are linked to the node P where odd-numbered nodes have a weight of two and even numbered nodes have a weight of one. W_P is called the weight of the node.

Your solveClientServer function must implement the following algorithm to set up and solve this linear system:

Create N_nbrs, a column vector containing the number of neighbors each node has (hint: use the sum command and the adjacency matrix)

Multiply the odd columns of the adjacency matrix by 2 (we'll call the result M_wt)

Calculate the vector of weights, W_p (hint: use the sum command and M_wt)

Set A (the coefficient matrix for the linear system) to be an appropriately-sized identity matrix

Set b (the right-hand side vector for the linear system) to be an appropriately-sized vector containing all ones

for each node N (i.e., for each row of A)

if N has only 1 neighbor (i.e., N is a client computer), then all that needs to be done is to set b(N) to 0

otherwise, N is a server, so we need to set the appropriate spots in the current row of A to the appropriate values.

multiply the corresponding row of M_wt by -1 and divide it by W_N (Note that this row of M_wt now has the appropriate coefficients for the nodes other than N in the equation for node N. )

add this row to the current row of A (which already contains the coefficient of 1 for node N)

Solve the linear system

D) The main program

The main program should go in your script and must implement the following algorithm:

ask the user for the name of the adjacency matrix file load the adjacency matrix from the file solve the linear system (using solveClientServer) use a for loop to display the results (in the format shown in the sample runs) 

You may assume that the file name entered by the user is the name of a file that does exist. You may also assume that any file you load is a text file containing a valid adjacency matrix.