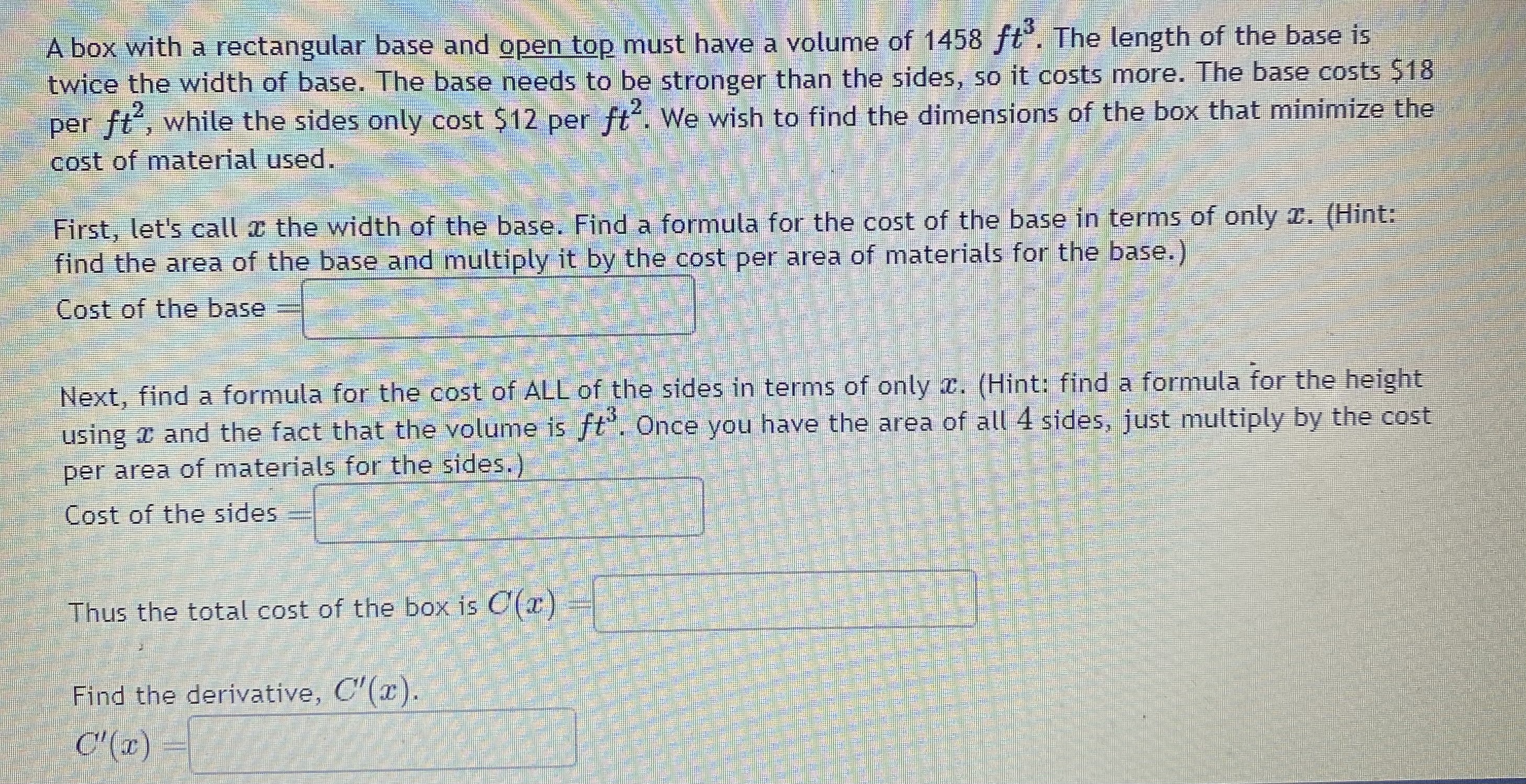
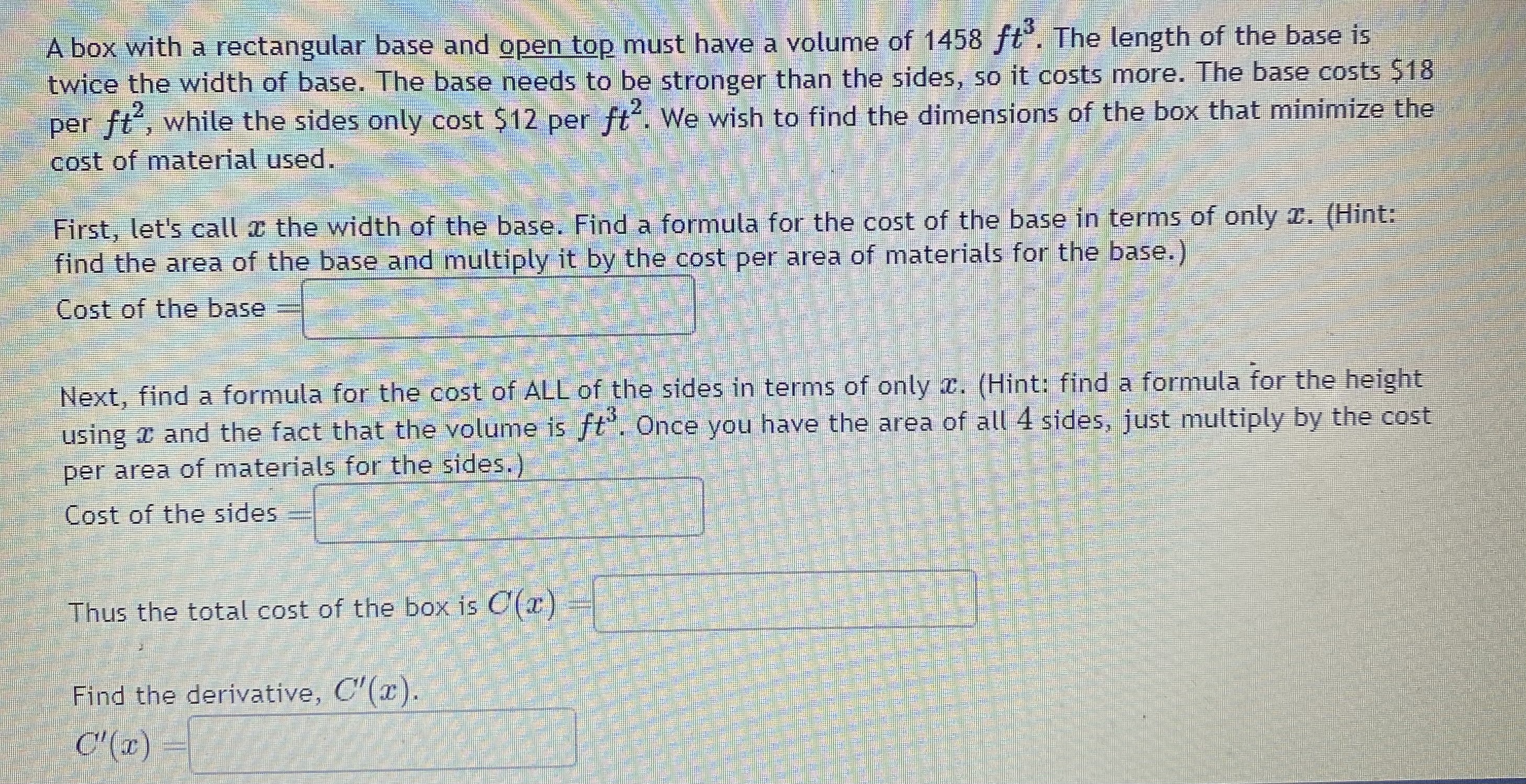
A box with a rectangular base and open top must have a volume of 1458 fto. The length of the base is twice the width of base. The base needs to be stronger than the sides, so it costs more. The base costs $18 per ft", while the sides only cost $12 per ft . We wish to find the dimensions of the box that minimize the cost of material used. First, let's call @ the width of the base. Find a formula for the cost of the base in terms of only c. (Hint: find the area of the base and multiply it by the cost per area of materials for the base.) Cost of the base Next, find a formula for the cost of ALL of the sides in terms of only c. (Hint: find a formula for the height using + and the fact that the volume is f . Once you have the area of all 4 sides, just multiply by the cost per area of materials for the sides.) Cost of the sides Thus the total cost of the box is O(a) Find the derivative, C''(x). C' (I)Now, calculate when the derivative equals zero, that is, when C'(x) = 0. C'(x) = 0 when r We next have to make sure that this value of @ gives a minimum value for the cost. Let's use the second derivative test. Find C"(x). C" (I)