Question: a) Compute the eigenvalues and eigenvectors of M b) Verify that v is an eigenvector of N. Note that you do not have to solve

a) Compute the eigenvalues and eigenvectors of M

b) Verify that v is an eigenvector of N. Note that you do not have to solve for the eigenvectors and also that the result may be somewhat approximate. Remember, what does it mean for it to be an eigenvector?

c) For the eigenvector in b), what is the corresponding eigenvalue (note, you do not need to solve for it. Hint: what does it mean that v is an eigenvector? Also note that it will be approximate (there may be a difference in the second or third decimal place.)

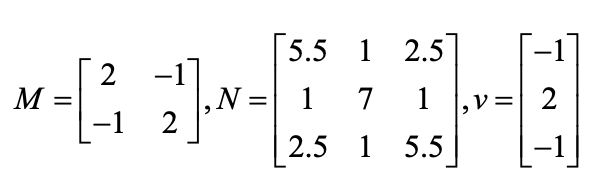
a) Compute the eigenvalues and eigenvectors of M b) Verify that v

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Introduction to MATLAB and Leslie Matrices 1) Start MATLAB 2) Create a 3x3 matrix named A with rows [1 2 3. 4, 5. 6], and 17, 8,9 3) You can also create functions in the command window. We will...

Problem ( 1. Create a 3 by 3 matrix M using the 8 digits of your student number and the number1 in the lower right entry. For example, if your student number is 12345678 then M- 4 5 6 Let A M +MT...

Any symmetric diagonalizable real valued matrix A in R* admits an eigenvalue decomposition of the following form: A = - UAUT, where the columns of U are orthonormal. This leads to a decomposition of...

Cuthill McKee algorithm Matlab function cluster _ custom _ rcm . m function C = cluster _ custom _ rcm ( A ) % Symmetrize adjacency matrix S = A + A ' ; % Reverse Cuthill - McKee ordering using your...

This question gives you a chance to work with the concept of spectral decomposition in a more intuitive way, using pictures. Matlab has a built-in test pattern image that we can use for this. Use the...

MATLAB PROGRAMMING Using the eigenvalue method of calculation, create a MATLAB program to compute and print out (using the MATLAB disp command) the following: a. Establish the mass and stiffness...

Subject- Optimization (a) Compute the eigenvalues and eigenvectors of the matrix A1=[1002] and show that the eigenvectors are orthogonal to each other. (b) Compute the eigenvalues and eigenvectors of...

Please give a step-by-step solution! Thank you! Consider the following rotation matrix R^ab that transforms vectors from frame f_b to f_a R^ab = [0.45457972 -0.34766601 0.82005221 0.43387382...

Construct a defective matrix by setting A = ones(6); A = A - tril(A) - triu(A, 2) It is easily seen that = 0 is the only eigenvalue of A and that its eigenspace is spanned by e1. Verify this by...

(4 pts) Given a system of differential equations 1 0 2 -1.8 0 0 5.1 0 -1 3 -CAD) X' = 1 2 -3 0 0X 0 1 -3.1 4 0 -2.8 0 0 1.5 1 Use Python to compute the eigenvalues and eigenvectors. Type the...

On June 1, 2018, Crane Company and Cheyenne Company merged to form Ayayai Inc. A total of 837,000 shares were issued to complete the merger. The new corporation reports on a calendar-year basis. On...

Read the Daniel Terris book. This will include an overview of Lockheed Martins organization and will lay out the research plan that Terris used to obtain information necessary for his work. This will...

A company evaluates that its risk of misappropriated funds ( stolen cash ) is severe enough that it needs a policy regarding the handling of cash. It has not yet implemented that policy. Which of the...

Problem 8 - 2 7 ( Algo ) Accounts receivable financing [ LO 8 - 1 ] Charming Paper Company sells to the 1 2 accounts IIsted here. \ table [ [ , \ table [ [ Receivable Balance ] , [ Outstanding ] ] ,...