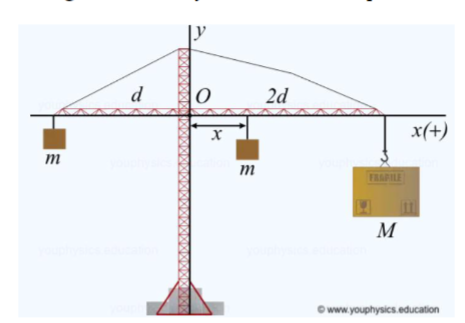
a crane whose arms have lengths d and 2d respectively. A mass m is fixed to the left and another mass m can move horizontally along the arms of the crane at a distance x from the vertical support. A third mass M is attached to the end of the right arm. The system is in static equilibrium. Using the Newton laws for statics equilibrium, it can be shown that the distance is given by =((2)/m)*d The load has a non-uniform mass density. After some computations, the mathematical expression to compute is obtained as a function of a variable : = 2 +10 100 =0 with 0 = 1 200() 40 =1 and if is even ()= (+^2sin ()/2^2 +1 if is odd ()= 2^2 +1/^2 +sin()

To compute the value of the load , you will first to compute the value 0. Write a Matlab script that asks the user for a valid value for d and m to find and print the value of 0. Note that i is in radians.

find all values of for 0 100. Deduce all corresponding values of . For 0 100, find and print how many times the controlling mass is on the left arm ( 0).