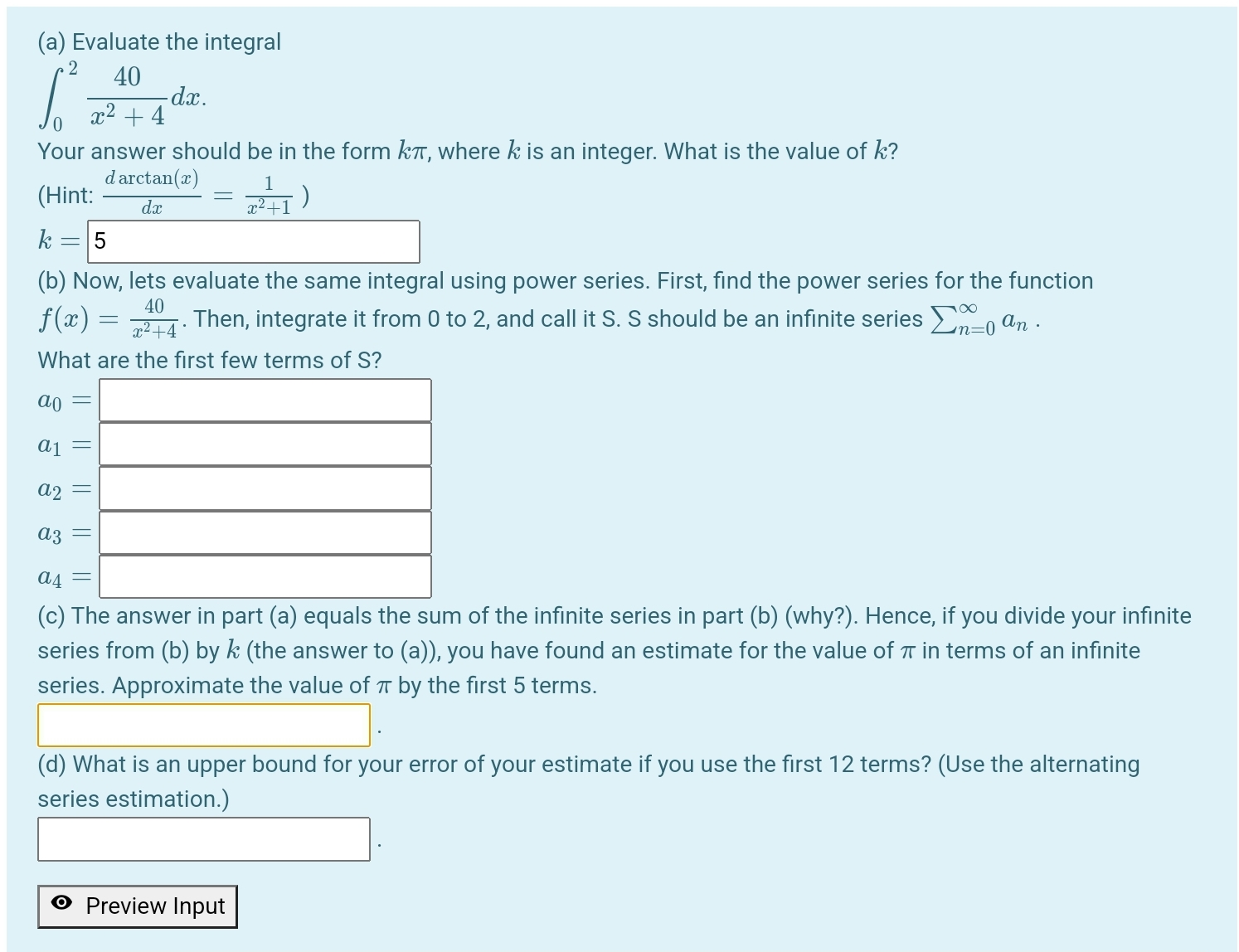
(a) Evaluate the integral 40 dx. 202 + 4 Your answer should be in the form k7, where k is an integer. What is the value of k? d arctan(x) (Hint: da 2 2 + 1 K 5 (b) Now, lets evaluate the same integral using power series. First, find the power series for the function f(2) = -2+. Then, integrate it from 0 to 2, and call it S. S should be an infinite series _= What are the first few terms of S? an a1 a3 a4 (c) The answer in part (a) equals the sum of the infinite series in part (b) (why?). Hence, if you divide your infinite series from (b) by k (the answer to (a)), you have found an estimate for the value of 7 in terms of an infinite series. Approximate the value of 7 by the first 5 terms. (d) What is an upper bound for your error of your estimate if you use the first 12 terms? (Use the alternating series estimation.) Preview Input