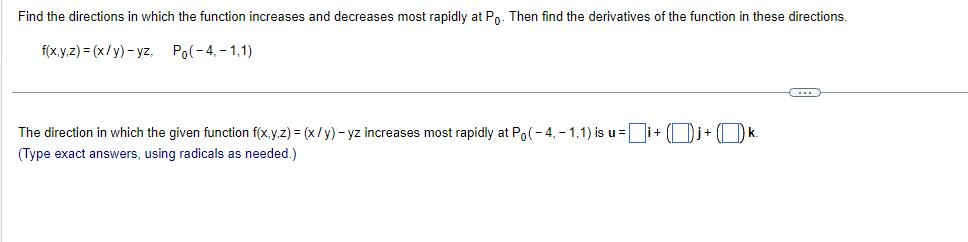
a

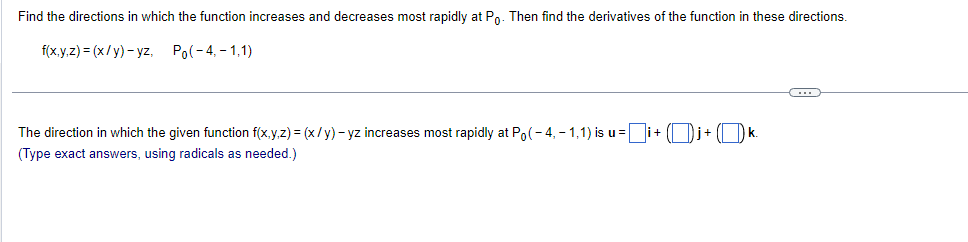
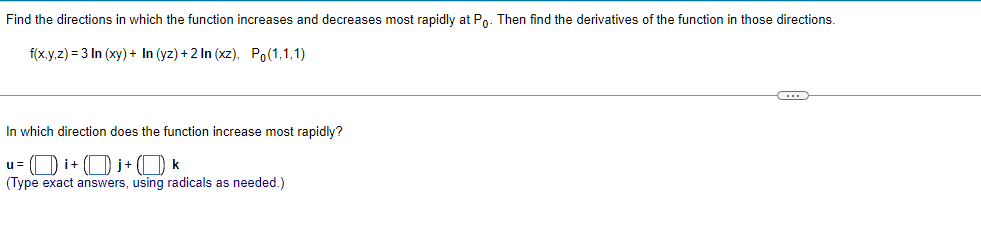
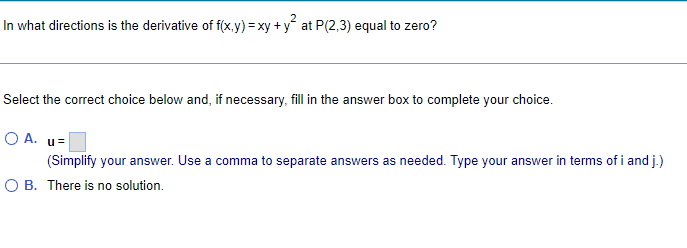
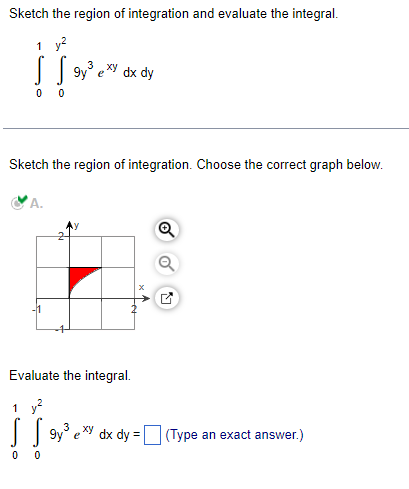
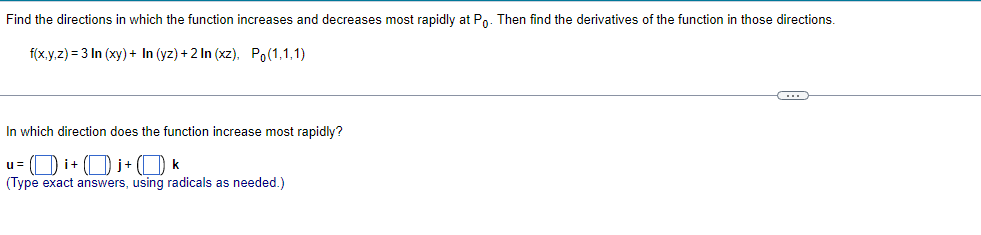
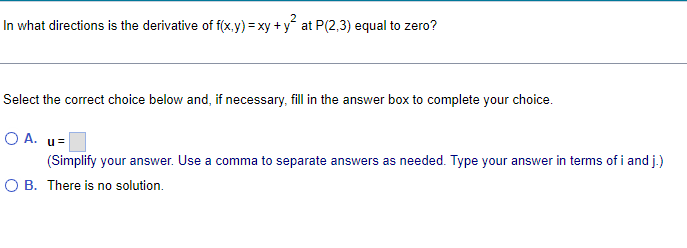
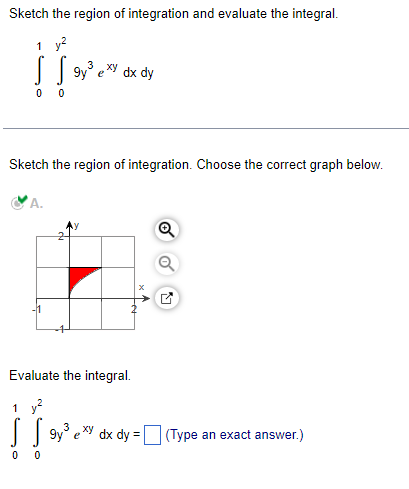
Find the directions in which the function increases and decreases most rapidly at Po. Then find the derivatives of the function in these directions. f(x,y,z) = (x/y) -yz. Po(-4, - 1,1) The direction in which the given function f(x,y,z) = (x/y) - yz increases most rapidly at Po( - 4, - 1,1) is u = i+ (Di + ()k. (Type exact answers, using radicals as needed.)Find the directions in which the function increases and decreases most rapidly at Po. Then find the derivatives of the function in those directions. f(x,y,z) = 3 In (xy) + In (yz) + 2 In (xz), Po(1,1,1) In which direction does the function increase most rapidly? u= ()i+ (0) )+()* (Type exact answers, using radicals as needed.)In what directions is the derivative of f(x,y) = xy + y at P(2,3) equal to zero? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. O A. u= (Simplify your answer. Use a comma to separate answers as needed. Type your answer in terms of i and j.) O B. There is no solution.Sketch the region of integration and evaluate the integral. dx dy 0 Sketch the region of integration. Choose the correct graph below. CA. AY X Evaluate the integral. 1 3 ey dx dy = (Type an exact answer.) 0 0