question below:

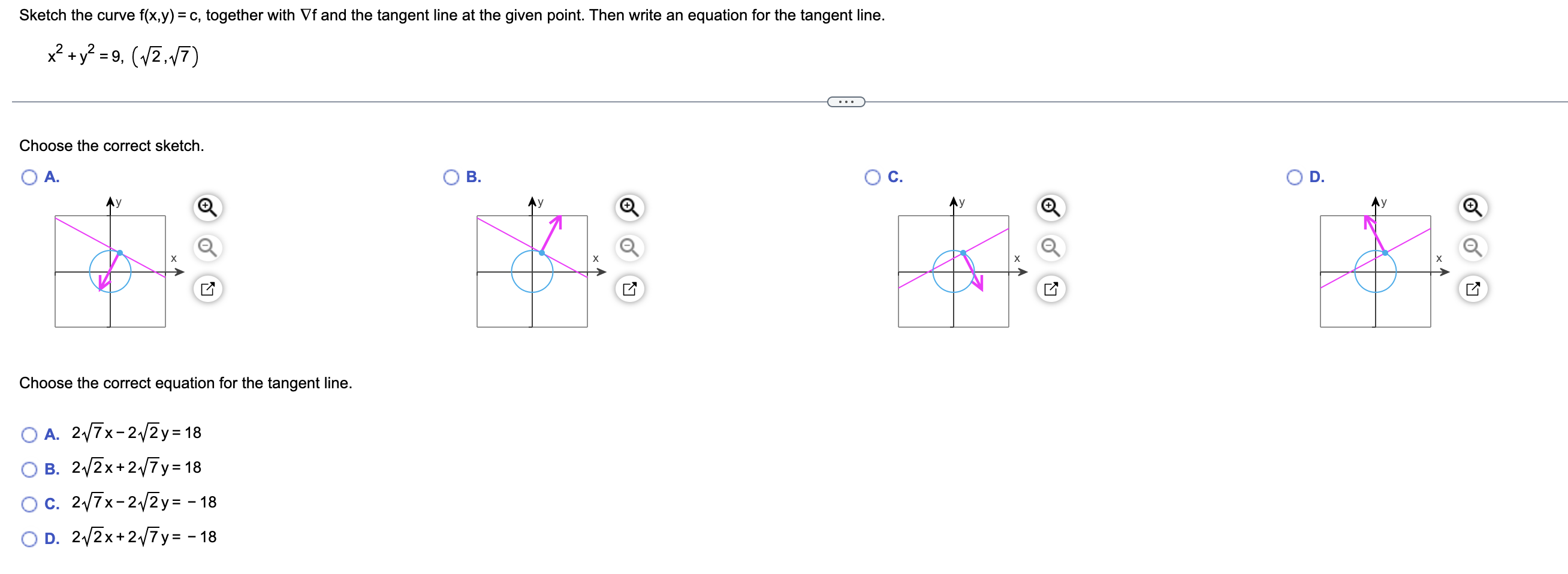
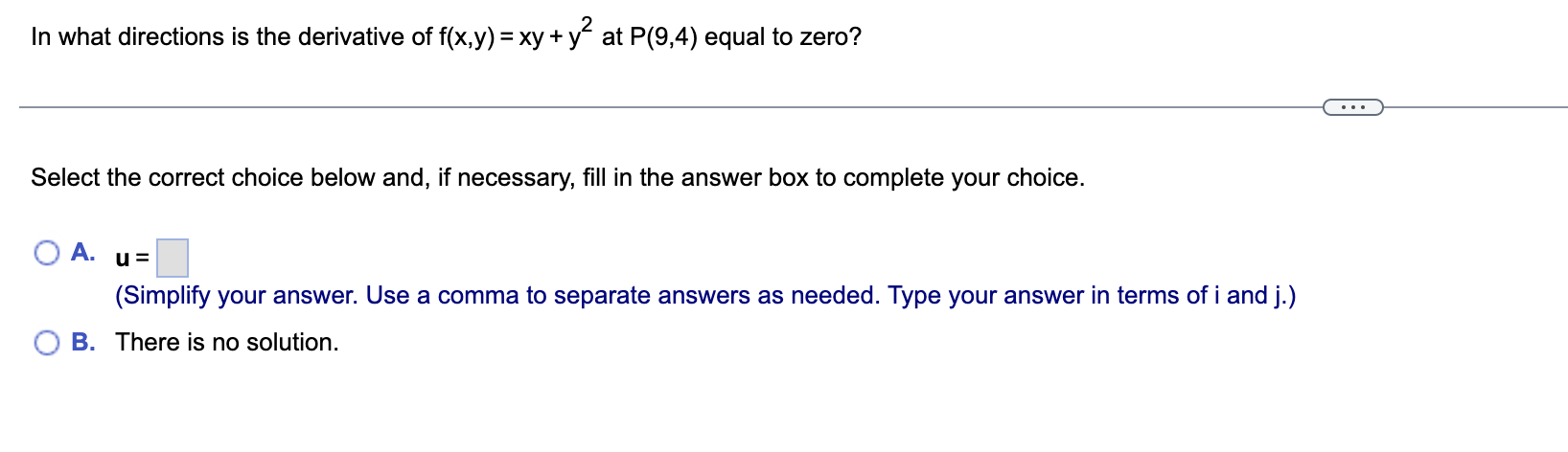
Find the directions in which the function increases and decreases most rapidly at P0. Then nd the derivatives of the function in these directions. le.y.Z)= (xly) -yz, Po(2, - 1, - 1) The direction in which the given function f(x,y,z) = (x/y) - yz increases most rapidly at Po(2, - 1, - 1) is u = i + (I j + ( J k. (Type exact answers, using radicals as needed.) The direction in which the given function f(x,y,z) = (x/y) - yz decreases most rapidly at Po(2, - 1, - 1) is - u = |i + (Dj + {D k. (Type exact answers, using radicals as needed.) The derivative of the given function f(x,y,z) = (x/ y) - yz in the direction in which the function increases most rapidly at Po(2, - 1, - 1) is (Duf) (2,_1'_ 1) = E. (Type an exact answer, using radicals as needed.) The derivative of the given function f(x,y,z) = (x/y) - yz in the direction in which the function decreases most rapidly at P0(2, - 1, - 1) is (D_ uf)(2.-1,-1) = Cl. (Type an exact answer, using radicals as needed.) Sketch the curve f(x.y) = 0, together with Vf and the tangent line at the given point. Then write an equation for the tangent line. x2+y2=a (4N7) Choose the correct sketch. o A. o a. o c. o n. v (6; Av (6;; Av