Question: A four-bar linkage system is shown below. The first link, a, is an input link (crank) of length 1m. The second link, b, is

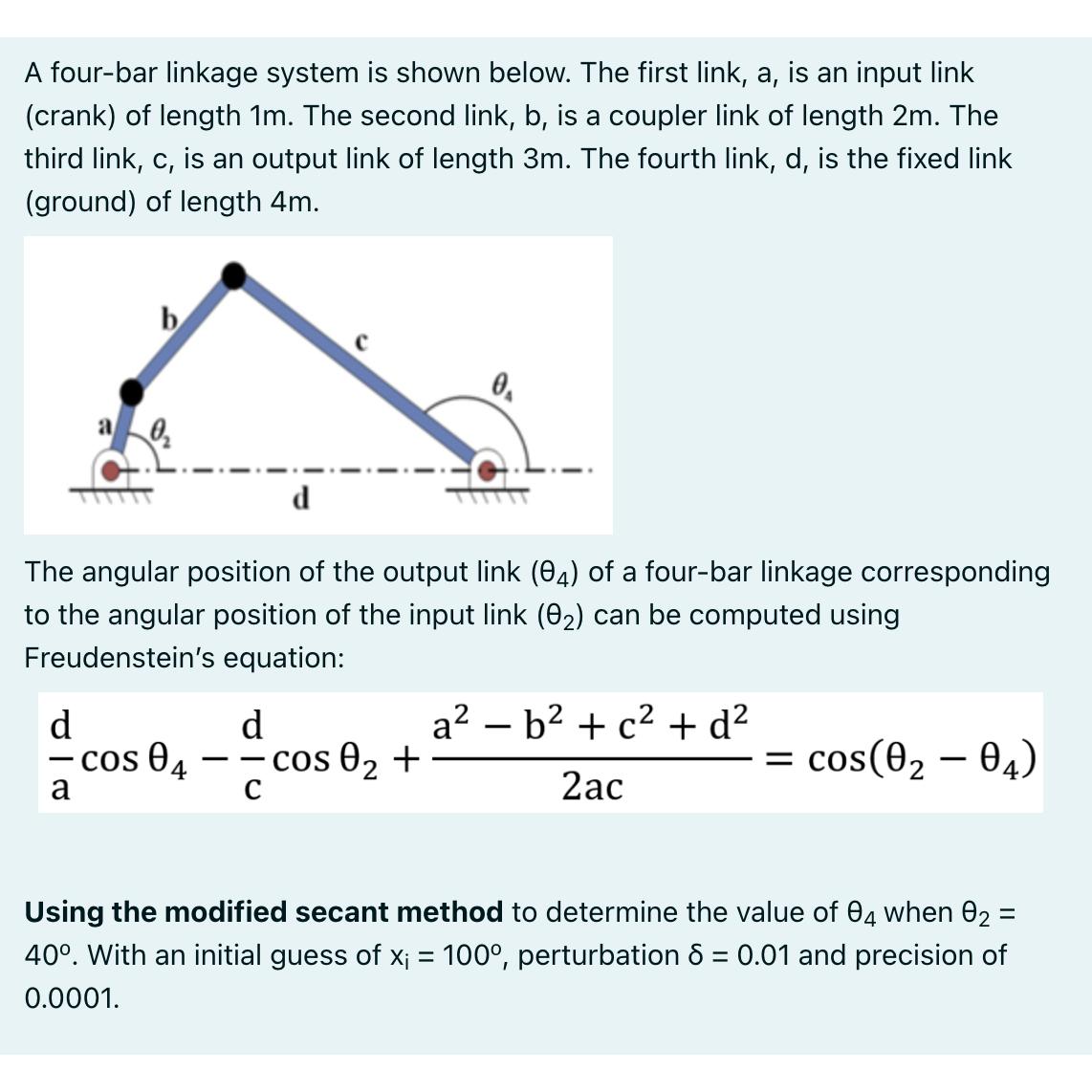
A four-bar linkage system is shown below. The first link, a, is an input link (crank) of length 1m. The second link, b, is a coupler link of length 2m. The third link, c, is an output link of length 3m. The fourth link, d, is the fixed link (ground) of length 4m. d - cos 04 a The angular position of the output link (84) of a four-bar linkage corresponding to the angular position of the input link (0) can be computed using Freudenstein's equation: d d - cos 0 + C 0 ab + c + d 2ac = cos(0 - 04) = Using the modified secant method to determine the value of 04 when 02 40. With an initial guess of x; = 100, perturbation 8 = 0.01 and precision of 0.0001.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

OutputMatlab code definition of the given function a 1b 2c 3d 4 t2 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Programming Questions!

An investigator took a random sample of Chief Financial Officers (CFOs) of public listed firms in Singapore, recorded their annual salaries and found that the salary distribution was skewed to the...

SummaryOnline BookwormsA preview of the page you will create is shown below.Instructions ?|Daniel Palmer is a content manager of Online Bookworms, a website dedicated to lovers of books and reading....

Adjustable-Rate and Subprime Mortgages The term subprime mortgage refers to mortgages given to home buyers with a heightened perceived risk of default, when, for instance, the price of the home being...

Objectives You will learn how to implement a class You will learn to use a header file You will learn how to create an object from a class you made Use a the vector class from the STL (Optional) ....

Q2: The figure shows a four-bar linkage (open configuration) that is driven by link O 2 A . All dimensions are in centimeters (cm). (The figure is not to scale) Find the following if 2 =55 o : The...

Rebecca is self-employed and earns $200,000 per year. If she makes a concessional contribution to superannuation of $8,000, how much tax (including Medicare Levy) will she save

B . Cylindrical pair C . Screw pair D . Flat pair The position of slider is R C = 2 0 i inch. The length for bar 1 and 3 are 1 3 and 7 inch, then angle is ? A . 0 B . 1 C . 2 D . 3 Grashof's Law...

Use MATLAB to calculate the four - bar linkage system and fulfill the following requirements 1 . Set the link lengths of 4 - bar linkage sequentially to be [ 5 , 2 , 4 , 6 ] and angular speed of the...

Write a script function called, yourlastnameGrashof, to determine the Grashof condition and state if input is a "crank or rocker' of a fourbar linkage system. The program must ask the user to input a...

A manufacturing company employs 14 project managers, 48 supervisors, and 377 laborers. In an effort to keep informed about any possible sources of employee discontent, management wants to conduct job...

Per the TAR Purchase and Sales Agreement, there is a period of time after the inspection period in which the parties can agree to any repairs. What is this period of time referred to as? Unset...

Researchers are interested in whether there is a difference between the number of brothers and number of sisters for graduate students. So they randomly selected 20 graduate students and asked each...

how would you compare the results between the lease assets vs total assets and the lease liabilities vs total liabilities visualization? finance lease assets are higher than finane lease liabilities...

You are an accounting associate assisting a compliance officer of a large private company. The compliance officer recently investigated concerns about accounting irregularities in journal entries...

A Pharmacy has four counter to serve Blood pressure test for customer. Customers arrive according to a Poisson distribution at the rate of 1 every 10 minutes. However, only 85% seek service at the...

Which Javascript function takes a string as a parameter and returns the string with the HTML tags removed?

Audrey purchases a riding lawnmower using a 2-year, no-interest deferred payment plan at Lawn Depot for x dollars. There was a down payment of d dollars and a monthly payment of m dollars. Express...

Sophia and Nic are operating a batch reactor at their grandfathers plant in Krls, Jofostan. The reaction is first-order, irreversible, liquid-phase, and exothermic. An inert coolant is added to the...

View the CSB video to list two things in which dust explosions are different from those involving flammable liquids.

Prepare a list of safety considerations for designing and operating chemical reactors. What would be the first four items on your list? For example, what safety concerns would you have for operating...

An investment advisor has worked with 24 clients for the past five years. Following are the percentage rates of average five-year returns that these 24 clients experienced over this time frame on...

USA Today reports salaries for National Football League (NFL) teams. The file Jaguars contains the salaries for the 2011 Jacksonville Jaguars. a. Calculate the average total salary for the...

Princess Cruises recently offered a 16-day voyage from Beijing to Bangkok during the time period from May to August. The announced price, excluding airfare, for a room with an ocean view or a balcony...