A graph G is 3-regular if every vertex has degree exactly 3, and a bridge is an edge that will divide a graph into two pieces if removed. A k-edge-coloring is a coloring of the edges of G with k colors such that no two edges that share an endpoint have the same color, as shown in Figure 4.13. Now consider the following conjecture, put forward by the Scottish mathematician and physicist Peter Guthrie Tait [770]:

Conjecture 4.2 Any planar, 3-regular graph without a bridge has a 3-edge-coloring.

Show that this conjecture is equivalent to the Four Color Theorem.

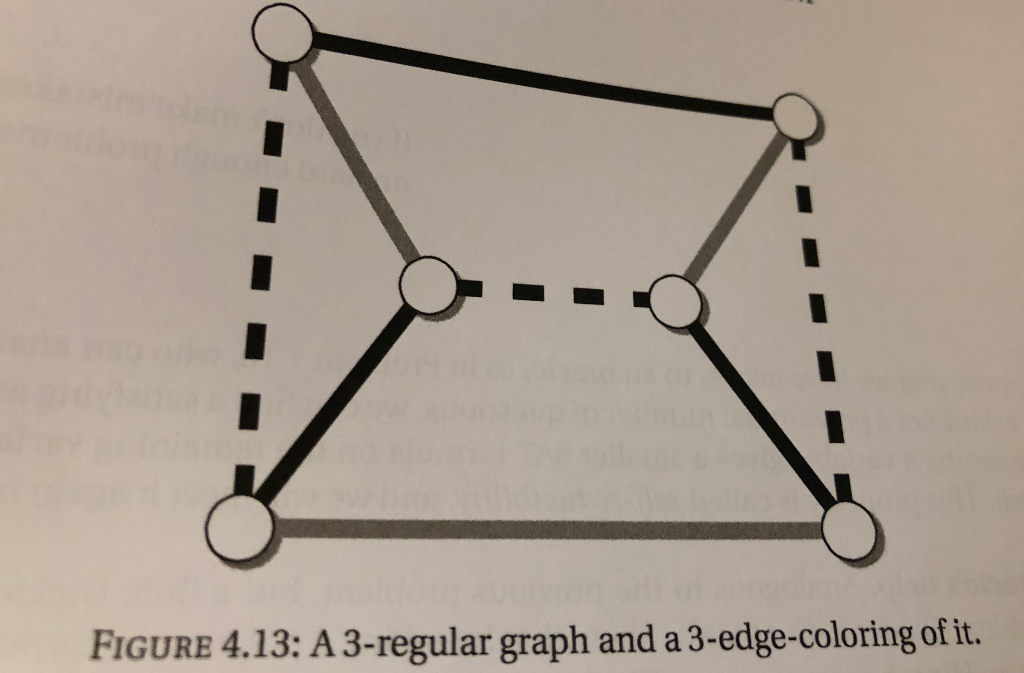
FIGURE 4.13: A 3-regular graph and a 3-edge-coloring of it