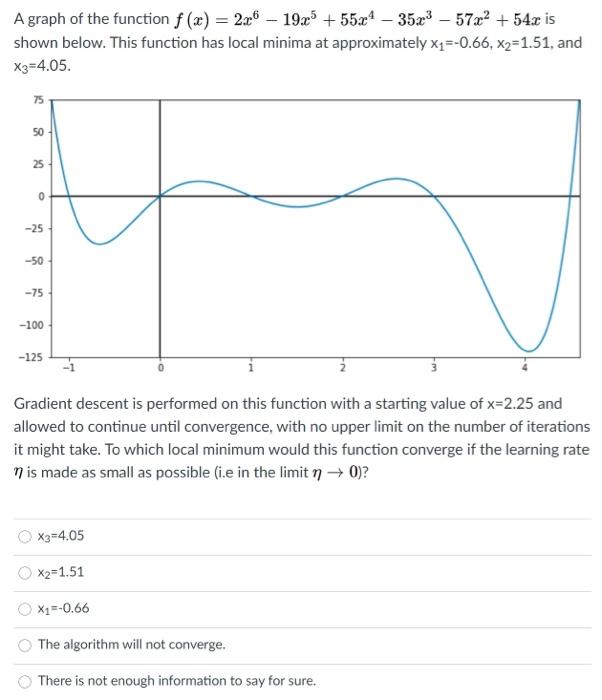
A graph of the function f (x) = 2.06 - 19x + 55x4 3523 572x + 54c is shown below. This function has local minima at approximately x1=-0.66, X2=1.51, and X3=4.05. 75 50 25 0 -25 -50 -75 -100 -125 Gradient descent is performed on this function with a starting value of x=2.25 and allowed to continue until convergence, with no upper limit on the number of iterations it might take. To which local minimum would this function converge if the learning rate n is made as small as possible (i.e in the limit n + 0)? X3 =4.05 X2=1.51 X1 =-0.66 The algorithm will not converge. There is not enough information to say for sure