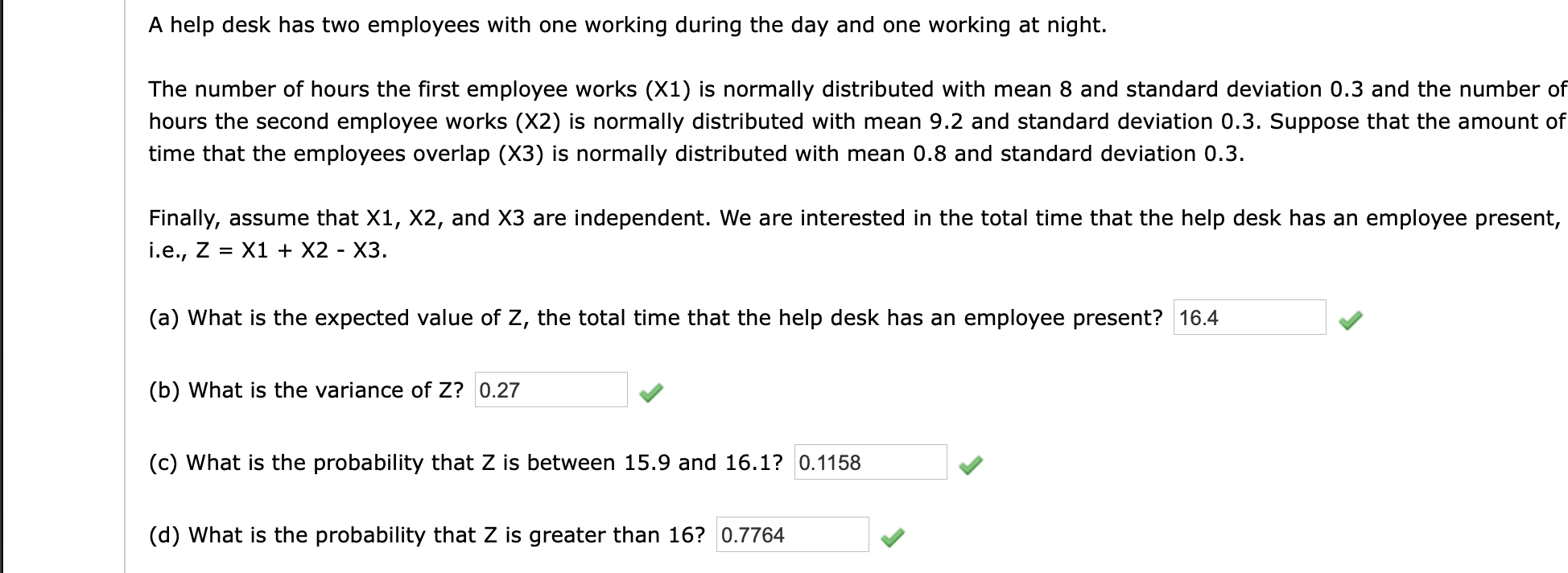
A help desk has two employees with one working during the day and one working at night. The number of hours the rst employee works (X1) is normally distributed with mean 8 and standard deviation 0.3 and the number of hours the second employee works (X2) is normally distributed with mean 9.2 and standard deviation 0.3. Suppose that the amount of time that the employees overlap (X3) is normally distributed with mean 0.8 and standard deviation 0.3. Finally, assume that X1, X2, and X3 are independent. We are interested in the total time that the help desk has an employee present, i.e., Z = X1 + X2 - X3. (a) What is the expected value of Z, the total time that the help desk has an employee present? 16.4 .I (b) What is the variance of Z? 0.27 J (c) What is the probability that Z is between 15.9 and 16.1? 0.1158 '1 (d) What is the probability that Z is greater than 16? 0.7764 1