Question: (a) Let (Xt)t0 be a stochastic process defined by 0tfrdWr,t0, where W=(Wr)r0 is a Wiener martingale and fH. Prove Cov(Xs,Xt)=E(XsXt)=E0tsfr2dr, for any s,t[0,), where st=min(s,t).

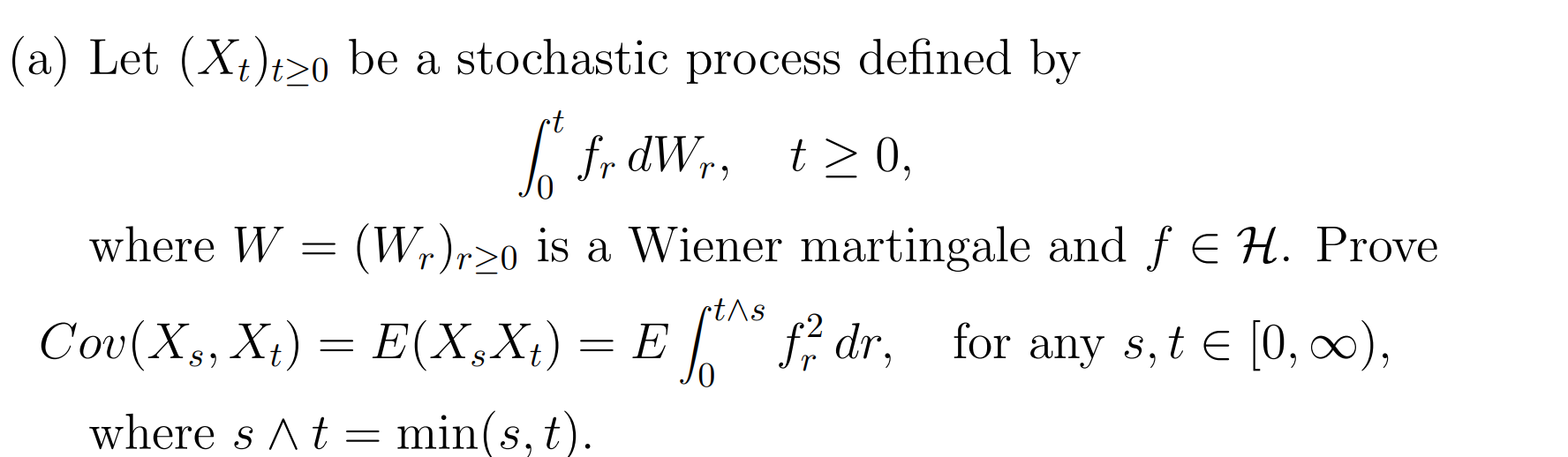
(a) Let (Xt)t0 be a stochastic process defined by 0tfrdWr,t0, where

(a) Let (Xt)t0 be a stochastic process defined by 0tfrdWr,t0, where W=(Wr)r0 is a Wiener martingale and fH. Prove Cov(Xs,Xt)=E(XsXt)=E0tsfr2dr, for any s,t[0,), where st=min(s,t). (a) Let (Xt)t0 be a stochastic process defined by 0tfrdWr,t0, where W=(Wr)r0 is a Wiener martingale and fH. Prove Cov(Xs,Xt)=E(XsXt)=E0tsfr2dr, for any s,t[0,), where st=min(s,t)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Finance Questions!

Let X(t), t0, be a discrete-valued random process with P{X(t) =k} = (At) e-At k! k N, " for some > 0. (a) Find E[X(t)]. (b) Is X(t) wide sense stationary? Explain why. (c) Assume t > t > 0. For k, k2...

Question 1 [ Total Marks: 4 0 ] Let x ( t ) = t , 0 t 1 2 t , 1 t 2 be a periodic signal with fundamental period T = 2 and Fourier series coefficients ak . a ) Determine the value of a 0 . b )...

Hi, I need some assistance for a question in a quiz from a course I take in Coursera. Compute the fair value of a chooser option which expires after n = 10 periods. At expiration the owner of the...

S Markov chains in continuous time. Let E be countable and G D .G.x; y//x;y2E a matrix satisfying the properties (i) G.x; y/ 0 for x y, (ii) a.x/ WD G.x; x/ (iii) a WD supx2E a.x/ We construct a...

only 1 question about financial engineering. please show your work Financial Engineering MRM 8610, Spring 2016 Homework 3 Daniel Bauer Due Thursday, 02/04/2016 before class. 1. Brownian Motion and...

Write 2 paragraphs about Effects of Covid-19 on Euro area GDP and inflation: demand vs. supply disturbances article. No max word count, page count, or formatting requirements but must be submit to my...

Problem 4: (30%) Consider the system , M f(t) K M = 4 kg, K 4 N/m, B =1 N-s/m Mx(t)+Bx(t)+ Kx(t) = f(t) with initial condition: x(0) = 0, x(0) = 0.2m (4a) The differential equation of MBK mechanical...

Let X(t) be a two-sided exponentially decaying signal defined as follows: (See figure below) x(t) = e-at t0 x(t) = - eat t

Eulers identity is very useful not only in obtaining the rectangular and polar forms of complex numbers, but in many other respects as we will explore in this problem. (a) Carefully plot x[n] = e jn...

1. Aircraft arrive at the maintenance center according to a Poisson process N(t) with pa- rameter A. In every aircraft a random number of parts is replaced according to a Poisson distribution with...

Fiscal year 2021 Transactions: d. On January 2, 2021, the City of Smithville approved the issuance of additional street improvement bonds in the total amount of $6,000,000. The new bonds will be...

a. Why are companies finding improprieties very expensive? b. What is the mission of ECOA? c. What kind of stature should an ethics officer hold within an organization? d. Research and summarize an...

Periodic interest rates. You have a savings account in which you leave the funds for one year without adding to or withdrawing from the account. Which would you rather have: a daily compounded rate...

9. (15 points) A company is considering a new project that requires an investment of \$5 million. The project is expected to generate cash flows of $2 million in year 1,$3 million in year 2, and $4...

1. Describe the types of power that effective leaders employ

2. Describe how leadership styles should be adapted to the group situation

7. Next time you work in a group, pay attention to how the group works. Does the activity follow a linear model, or is the activity punctuated by periods of inertia and periods of intense activity?...