a)

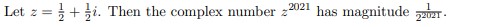
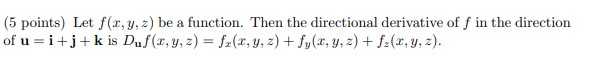
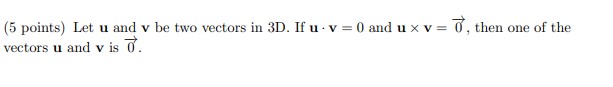
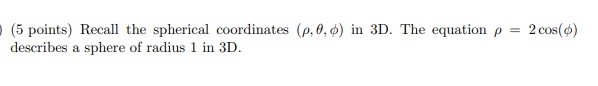
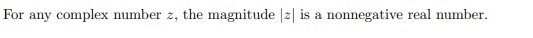
Let z = + si. Then the complex number 2021 has magnitude 1(5 points) Let f(, y, z) be a function. Then the directional derivative of f in the direction of u = i+ j + k is Duf(x, y, 2) = f(r, y, 2) + fy(2, y.=)+ (r,y, =).(5 points) Let u and v be two vectors in 3D. If u - v = 0 and u x v = 0, then one of the vectors u and v is o.(5 points) Recall the cylindrical coordinates (r, 0, 2) in 3D. The equation & = = describes a half-plane in 3D.(5 points) Recall the spherical coordinates (p, 0, () in 3D. The equation p = 2 cos($) describes a sphere of radius 1 in 3D.(5 points) Consider the function for (x, y) / (0, 0), f(x, y) 0 for (x, y) = (0, 0). Then f is continuous at (0, 0).(5 points) Let A be the subset of 2D with points (x, y) such that r