Question: A linear programming computer package is needed. Romans Food Markek, located in Saratoga, New York, carries a variety of specialty foods from around the world.
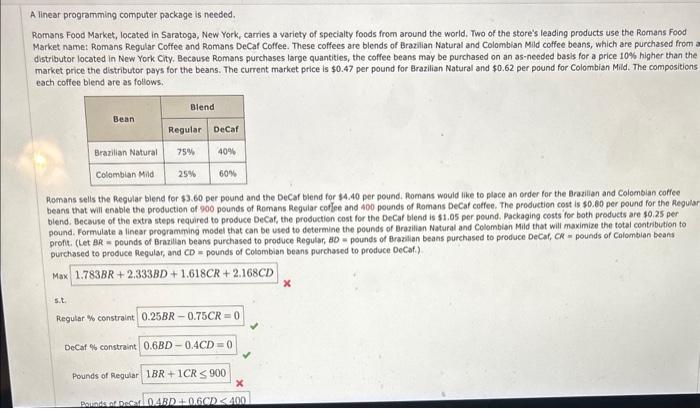

A linear programming computer package is needed. Romans Food Markek, located in Saratoga, New York, carries a variety of specialty foods from around the world. Two of the store's leading products use the Romans Food Market name: Romans Regular Coffee and Romans DeCaf Coffee. These coffees are blends of Brazilan Natural and Colombian Mild coffee beans, which are purchased from a distributor located in New York City. Because Romans purchases large quantities, the coffee beans may be purchased on an as-needed basis for a price 10\% higher than the market price the distributor pays for the beans. The current market price is $0.47 per pound for Brazilian Natural and $0.62 per pound for Colombian Mild. The compositions each coffee blend are as follows. Romans sells the Regular blend for $3.60 per pound and the DeCaf blend for $4.40 per pound. Aomans would like to place an order for the Brazillan and Colombian coffee beans that will enable the production of 900 pounds of Romans Regular cof 5 ee and 400 pounds of Romans DeCaf cotfee. The production cost is $0.60 per pound for the Regular blend. Because of the extra steps required to produce DeCat, the production cost for the DeCar biend is 51.05 per pound. Packaging costs for both products are $0.25 per pound. Formulate a linear programming model that can be used to determine the pounds of Brazilian Natural and Colombian Mild that will maximize the total contribution to proft. (Let BR = pounds of Brazillan beans purchased to produce Regutar, BD= pounds of Brazilian beans purchased to produce DeCaf, CR= pounds of Colombian beans purchased to produce flegular, and CD= pounds of Colombian beans porchased to produce DeCaf.) Max profit. (Let BR= pounds of Brazilian beans purchased to produce Regular, BD= pounds of Brazilian beans purchased to p purchased to produce Regular, and CD= pounds of Colombian beans purchased to produce DeCaf.) Max s.t. Regular % constraint DeCaf % constraint Pounds of Regular Pounds of DeCaf What is the optimal solution and what is the contribution to profit (in $ )? (Round your contribution to profit to two decimal pl (BR,BD,CR,CD)Profit==$x A linear programming computer package is needed. Romans Food Markek, located in Saratoga, New York, carries a variety of specialty foods from around the world. Two of the store's leading products use the Romans Food Market name: Romans Regular Coffee and Romans DeCaf Coffee. These coffees are blends of Brazilan Natural and Colombian Mild coffee beans, which are purchased from a distributor located in New York City. Because Romans purchases large quantities, the coffee beans may be purchased on an as-needed basis for a price 10\% higher than the market price the distributor pays for the beans. The current market price is $0.47 per pound for Brazilian Natural and $0.62 per pound for Colombian Mild. The compositions each coffee blend are as follows. Romans sells the Regular blend for $3.60 per pound and the DeCaf blend for $4.40 per pound. Aomans would like to place an order for the Brazillan and Colombian coffee beans that will enable the production of 900 pounds of Romans Regular cof 5 ee and 400 pounds of Romans DeCaf cotfee. The production cost is $0.60 per pound for the Regular blend. Because of the extra steps required to produce DeCat, the production cost for the DeCar biend is 51.05 per pound. Packaging costs for both products are $0.25 per pound. Formulate a linear programming model that can be used to determine the pounds of Brazilian Natural and Colombian Mild that will maximize the total contribution to proft. (Let BR = pounds of Brazillan beans purchased to produce Regutar, BD= pounds of Brazilian beans purchased to produce DeCaf, CR= pounds of Colombian beans purchased to produce flegular, and CD= pounds of Colombian beans porchased to produce DeCaf.) Max profit. (Let BR= pounds of Brazilian beans purchased to produce Regular, BD= pounds of Brazilian beans purchased to p purchased to produce Regular, and CD= pounds of Colombian beans purchased to produce DeCaf.) Max s.t. Regular % constraint DeCaf % constraint Pounds of Regular Pounds of DeCaf What is the optimal solution and what is the contribution to profit (in $ )? (Round your contribution to profit to two decimal pl (BR,BD,CR,CD)Profit==$x
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


