A Matlab introductory class Problem.

The book for my class is "Introduction to MATLAB For Engineers, Third edition by William J. Palm

There are 3 parts to this problem, I completed one of the three, which is creating a function that takes in two arrays and returns an array that is the derivative of the second. I called it Derivatron (as told to do so in the problem. )

Here is what I have so far

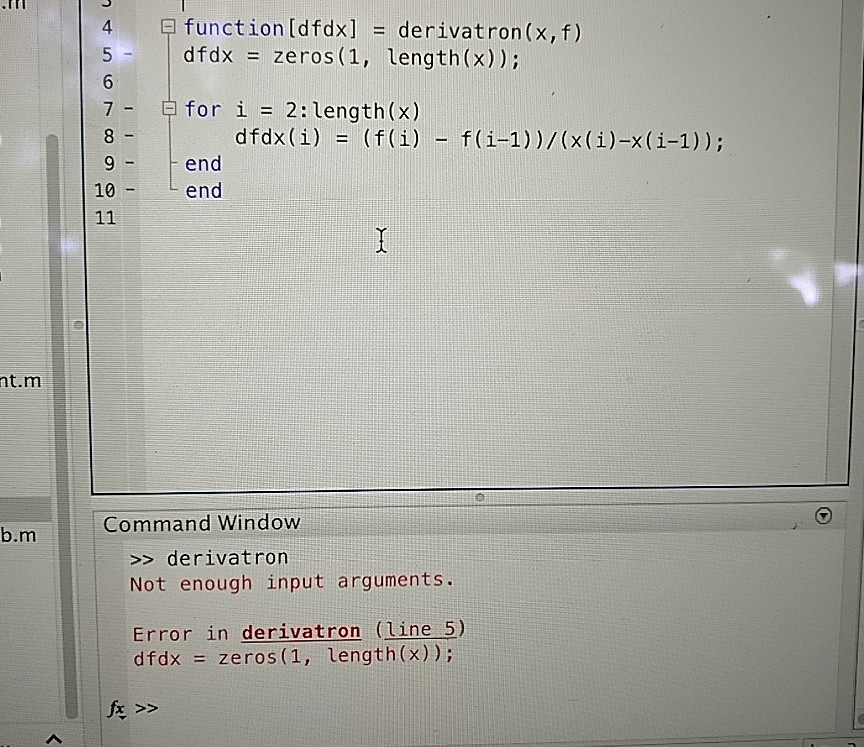
I would like to be helped on step 2 and 3

Thank You I will give a thumbs up if you answer me this problem.

THE DERIVATRON EGME 205, Fall 2018 A derivative is defined as: 7 November 2018 df-lim fle + )-f(2) If df /dr is particularly difficult to evaluate, a finite approximation can be reasonable: dz which, for small A, can be close to the 'actual' value of the derivative. In array form, 1 Assembling the Derivatron Write a function that takes in two arrays and returns an array that is the derivative of the second (ie, the f or y array) with respect to the first (ie, the x or y) array. Call the function derivatron. 2 Swimming in Sine Test your derivatron function to show that the derivative of sin z is cos z and the derivative of cos r is -sin r. Create two figures. One plotting cosz and-sin directly from 0 to 2 and the other plotting the calculated derivatives of sin z and cos r over the same interval 3 Easy Rocket Science A rocket's velocity, from launch (t -0) to t 100s is given by V) -17 00001- 0.004 Use your derivatron to estimate the acceleration. Use your integratron to estimate the distance traveled. On a 3x1 subplots figure, graph the position in the top axes, the velocity in the middle, and the acceleration in the bottom. Provide suitable axis labels. It may be worth manually taking the derivative/ integral of velocity to compare to your numerical- approximation results! Notes Make your figures interesting, clear, and well-scaled. Save your derivatron on a flash drive or cloud storage so it is accessible to you for later THE DERIVATRON EGME 205, Fall 2018 A derivative is defined as: 7 November 2018 df-lim fle + )-f(2) If df /dr is particularly difficult to evaluate, a finite approximation can be reasonable: dz which, for small A, can be close to the 'actual' value of the derivative. In array form, 1 Assembling the Derivatron Write a function that takes in two arrays and returns an array that is the derivative of the second (ie, the f or y array) with respect to the first (ie, the x or y) array. Call the function derivatron. 2 Swimming in Sine Test your derivatron function to show that the derivative of sin z is cos z and the derivative of cos r is -sin r. Create two figures. One plotting cosz and-sin directly from 0 to 2 and the other plotting the calculated derivatives of sin z and cos r over the same interval 3 Easy Rocket Science A rocket's velocity, from launch (t -0) to t 100s is given by V) -17 00001- 0.004 Use your derivatron to estimate the acceleration. Use your integratron to estimate the distance traveled. On a 3x1 subplots figure, graph the position in the top axes, the velocity in the middle, and the acceleration in the bottom. Provide suitable axis labels. It may be worth manually taking the derivative/ integral of velocity to compare to your numerical- approximation results! Notes Make your figures interesting, clear, and well-scaled. Save your derivatron on a flash drive or cloud storage so it is accessible to you for later