(a) Maximum reliability = _________________ (b) Optimal # of spares for subsystem 1 = ______________ (c) Optimal # of spares for subsystem 2 = ______________ (d) Optimal # of spares for subsystem 3 = ______________

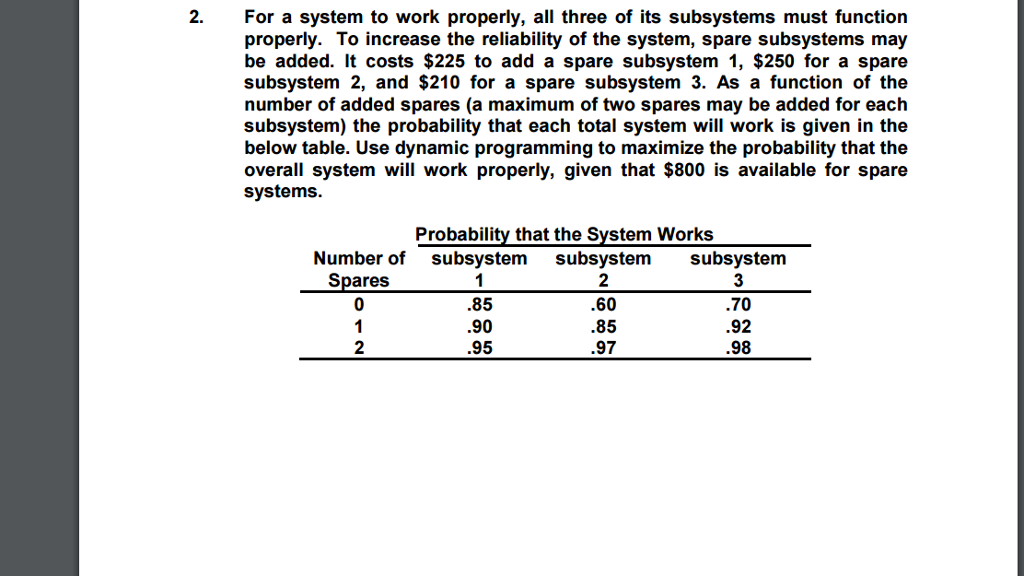
2. For a system to work properly, all three of its subsystems must function properly. To increase the reliability of the system, spare subsystems may be added. It costs $225 to add a spare subsystem 1, $250 for a spare subsystem 2, and $210 for a spare subsystem 3. As a function of the number of added spares (a maximum of two spares may be added for each subsystem) the probability that each total system will work is given in the below table. Use dynamic programming to maximize the probability that the overall system will work properly, given that $800 is available for spare systems. Probability that the System Works Number of subsystem subsystem subsystem Spares 85 60 70 90 85 92 .97 .98 95