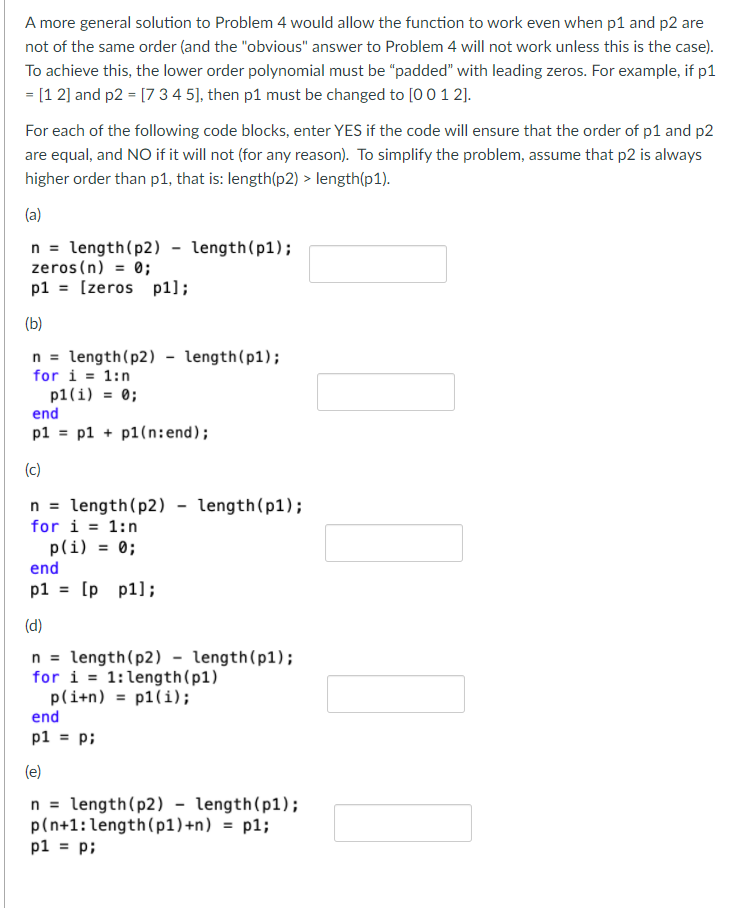
A more general solution to Problem 4 would allow the function to work even when p1 and p2 are not of the same order (and the "obvious" answer to Problem 4 will not work unless this is the case). To achieve this, the lower order polynomial must be "padded" with leading zeros. For example, if p1 = [1 2] and p2 = [7 3 4 5), then p1 must be changed to [0 0 1 2]. For each of the following code blocks, enter YES if the code will ensure that the order of p1 and p2 are equal, and NO if it will not (for any reason). To simplify the problem, assume that p2 is always higher order than p1, that is: length(p2) > length(p1). (a) n = length(p2) - length(p1); zeros(n) = 0; p1 = (zeros p1]; (b) n = length(p2) - length(p1); for i = 1:n p1(i) = 0; end p1 = p1 + p1(n:end); (c) n = length(p2) - length(p1); for i = 1:n p(i) = 0; end p1 = [p p1]; (d) n = length(p2) - length(p1); for i = 1: length(p1) p(i+n) = p1(i); end p1 = p; (e) n = length(p2) - length(p1); p(n+1: length(p1)+n) = p1; p1 = p