A parallel-plate capacitor of capacitance C with circular plates is charged by a constant current I . The radius a of the plates is much larger than the distance d between them, so fringing effects are negligible. Calculate B(r) , the magnitude of the magnetic field inside the capacitor as a function of distance from the axis joining the center points of the circular plates.

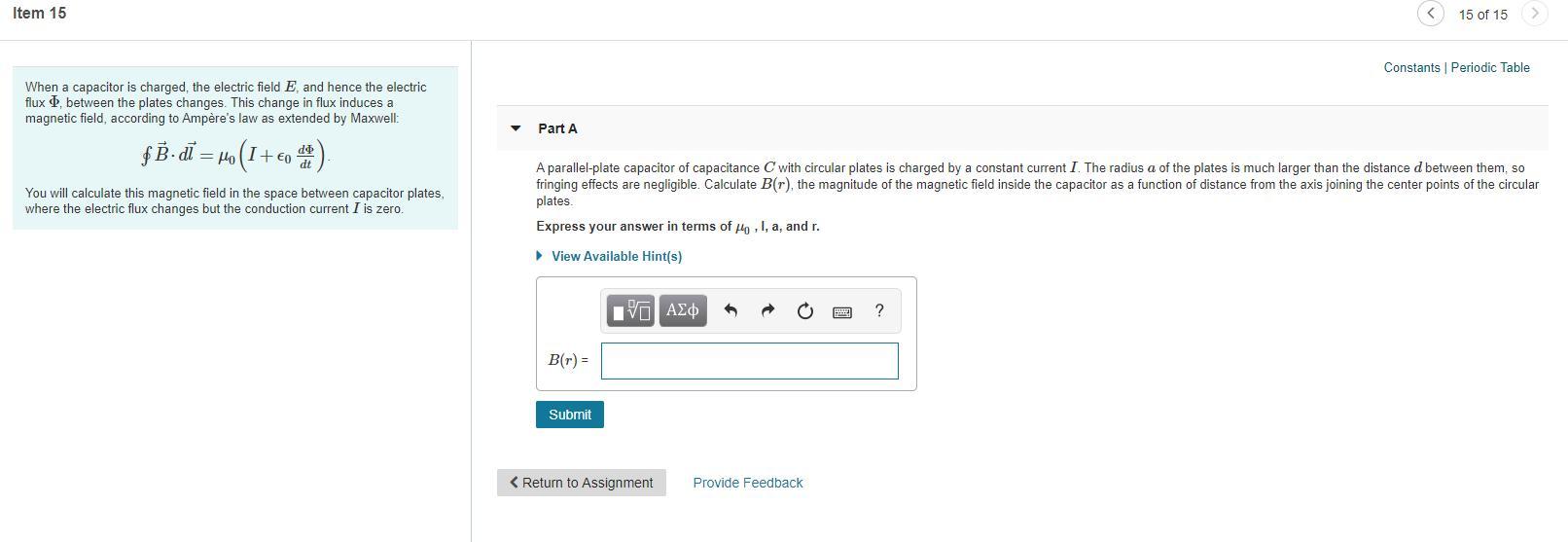
Item 15 15 of 15 Constants | Periodic Table When a capacitor is charged, the electric field E, and hence the electric flux 4, between the plates changes. This change in flux induces a magnetic field, according to Ampre's law as extended by Maxwell: Part A f B- a = , (1+co ) A parallel-plate capacitor of capacitance C with circular plates is charged by a constant current I. The radius a of the plates is much larger than the distance d between them, so fringing effects are negligible. Calculate B(r), the magnitude of the magnetic field inside the capacitor as a function of distance from the axis joining the center points of the circular plates. You will calculate this magnetic field in the space between capacitor plates, where the electric flux changes but the conduction current I is zero. Express your answer in terms of n , 1, a, and r. View Available Hint(s) B(r) = Submit < Return to Assignment Provide Feedback Item 15 15 of 15 Constants | Periodic Table When a capacitor is charged, the electric field E, and hence the electric flux 4, between the plates changes. This change in flux induces a magnetic field, according to Ampre's law as extended by Maxwell: Part A f B- a = , (1+co ) A parallel-plate capacitor of capacitance C with circular plates is charged by a constant current I. The radius a of the plates is much larger than the distance d between them, so fringing effects are negligible. Calculate B(r), the magnitude of the magnetic field inside the capacitor as a function of distance from the axis joining the center points of the circular plates. You will calculate this magnetic field in the space between capacitor plates, where the electric flux changes but the conduction current I is zero. Express your answer in terms of n , 1, a, and r. View Available Hint(s) B(r) = Submit < Return to Assignment Provide Feedback