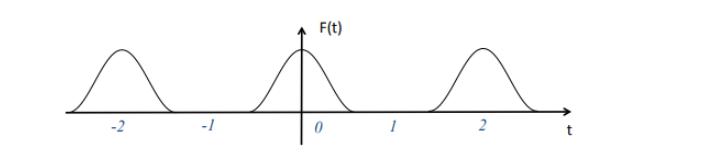
A pictured function has Fourier series representation on F(t) = 0 + a, cos (2x) + b, sin (2x) n=1 T n=1 You are not asked to calculate the Fourier coefficients an and br T a) What is the period T? (3) b) Based on the plot of F(t), what can you say about the coefficients ao, a and b? Do any vanish? c) This force is applied to a simple damped oscillator m+cx+kx = F(t). (4) Find the steady-state response Ist-st (t), i.e. the response after a long time has passed. Leave your answer in terms of the ao, an, bn and the system parameters m, k, c, and any secondary variables you may have defined in terms of them (like or or w, or wa or G - make sure you do define any you use). d) What is the average position of the oscillator after a long time has passed? 2 F(t) -1 0 2