A pond drains through a pipe as shown below. Under a number of simplifying assumptions, the following differential equation describes how depth changes with time:

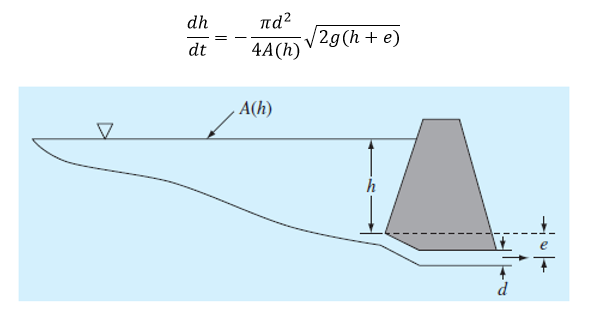
Where h = depth (m), t = time (s), d = pipe diameter (m), A(h) = pond surface area as afunction of depth (m²), g =gravitational constant (= 9.81 m/s²), and e = depth of pipeoutlet below the pond bottom (m). Based on the following area-depth table, solve this differential equation to determine how long it takes for the pond to empty, given that:

h(0) = 6 m, d = 0.25 m, e = 1 m.

h (m)	6	5	4	3	2	1	0
A(h) x 104 m2	1.17	0.97	0.67	0.45	0.32	0.18

Hint:

1. Fit a fifth-order polynomial with a zero intercept for the area-depth data [Note that the Excel curve-fitting equation is not accepted];

2. Substitute the derived polynomial into the differential equation given above;

3. Solve (integrate) the derived equation at step 2 numerically (using Eulers method Modified Eulers method, and Runge-Kutta method and h=0.025). Details of three steps for each method are required then a computer code can be developed for the rest of iterations.

Develop a computer code (MATLAB) for step 3. Terminate the program running when a negative area is detected.

dh d2 dt 4A(h) ATh5V2g(h +e) A(h) e T t-fd Td h- It