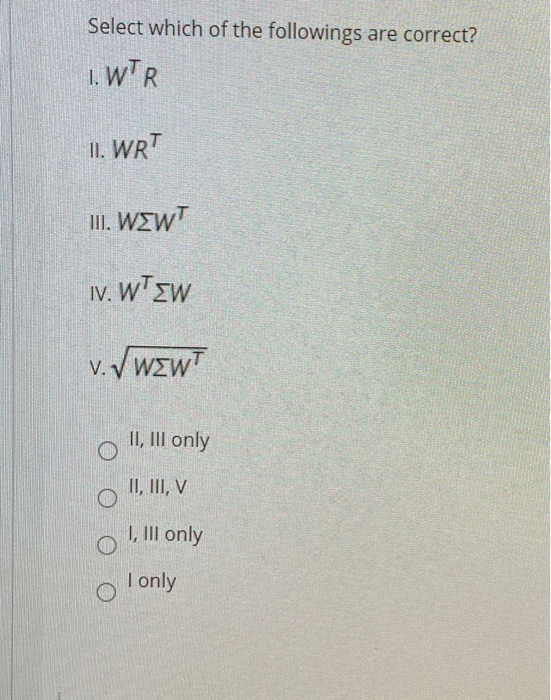
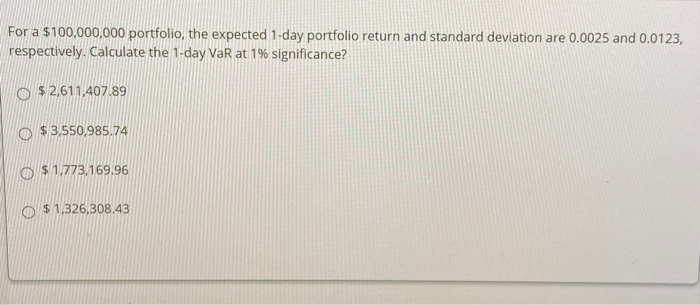
A portfolio return and portfolio standard deviation (variance) can be computed using matrix multiplication. Given that a weight vector, w=(w_1,w_2,w_3), a return vector, R= (r_1,r_2, 3), and a covariance matrix, o 01,201,3 [= 02,1 02 02,3 03.1 03,20 Select which of the followings are correct? Select which of the followings are correct? 1. WTR. 11. WRT III. WEWT iv. WTEW V.VWEWT II, III only O II, III, V I, III only I only For a $100,000,000 portfolio, the expected 1-day portfolio return and standard deviation are 0.0025 and 0.0123, respectively. Calculate the 1-day VaR at 1% significance? $ 2,611,407.89 $ 3,550.985.74 o $ 1.773,169.96 $ 1,326,308,43 Your investment has a 40% chance of earning a 15% rate of return, a 50% chance of earning a 10% rate of return, and a 10% chance of losing 3%. What is the standard deviation of this investment? O 8.43% O 7.59% 9.29% O 5.14%