A primal linear program has constraints

$2x_1+x_{2}10,$

$x_1+2x_{2}10,$

$-x_1+2x_{2}6,$

$x_1,x_{2}0.$

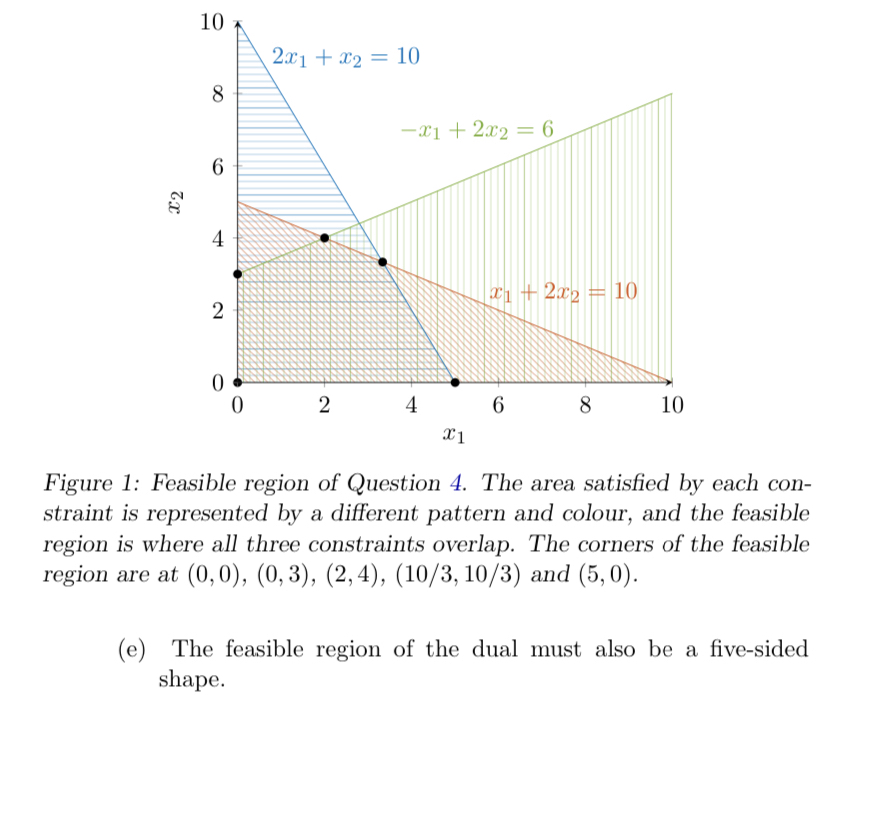
Figure $1$ illustrates the feasible region.

Determine whether the following statements are true or false and justify your answer. No marks will be awarded if your answer is not justified.

$($a$)$ One of many possible optimal solutions is $(x_1,x_2)=(2,2),$ but we cannot be sure if we do not know the objective function.

$($b$)$ If the optimal solution of the linear program is at $(x_1,x_2)=(0,0),$ then the optimal solution of the dual also has all decision variables equal to zero.

$($c$)$ For one given objective, the optimal solution could be at $(x_1,x_2)=(2,4)$ and at $(x_1,x_2)=(\frac{10}{3},\frac{10}{3}).$

$($d$)$ Depending on the objective, this linear program could be infeasible.

Figure $1$: Feasible region of Question $4.$ The area satisfied by each constraint is represented by a different pattern and colour, and the feasible region is where all three constraints overlap. The corners of the feasible region are at $(0,0),(0,3),(2,4),(\frac{10}{3},\frac{10}{3})$ and $(5,0).$

$($e$)$ The feasible region of the dual must also be a five$-$sided shape.