Question: A radioactive element decays according to the function ( mathrm { Q } = mathrm { Q } _ { 0 }
A radioactive element decays according to the function mathrmQmathrmQ emathrmrt where mathrmQ is the amount of the substance at time mathrmtmathrmr is the continuous compound rate of decay, t is the time in years, and Q is the amount of the substance at time t If the continuous compound rate of the element per year is r how long will it take a certain amount of this element to decay to half the original amount?
The period is the halflife of the substance.
The halflife of the element is approximately years.
Do not round until the final answer. Then round to the nearest year as needed.
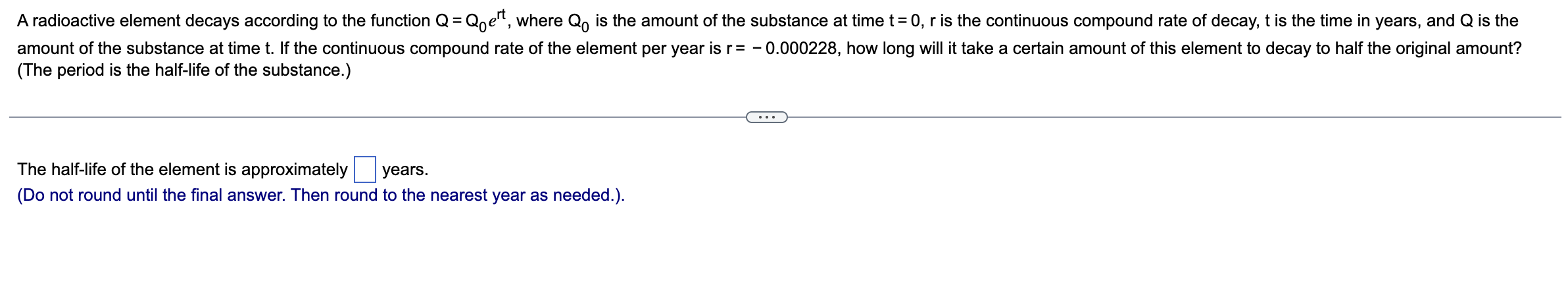
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


