Question: A region bounded by f(x) = -x2 + 5, y = 1, and x = O is shown below. Find the volume of the solid

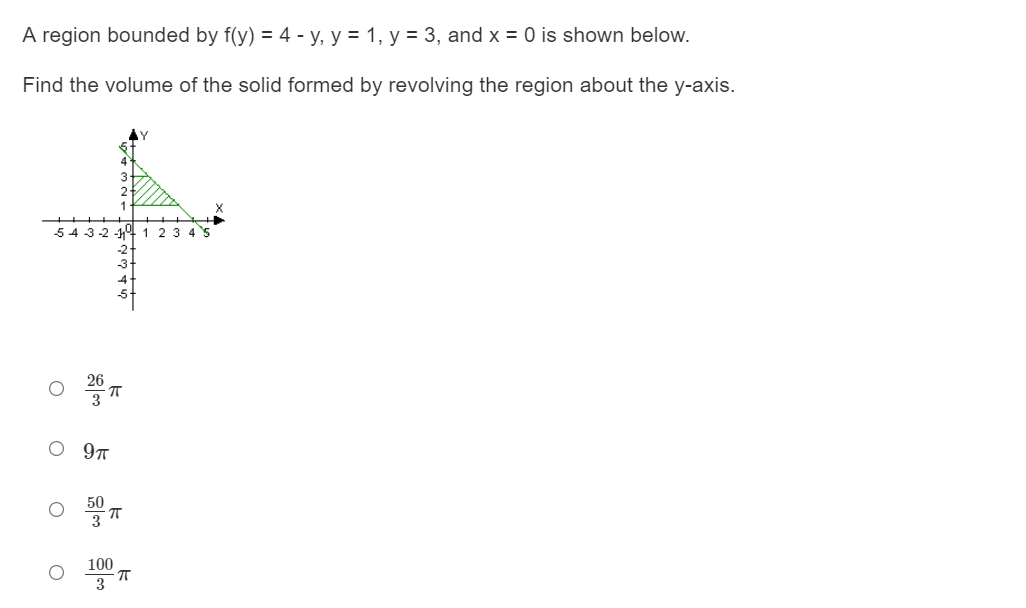





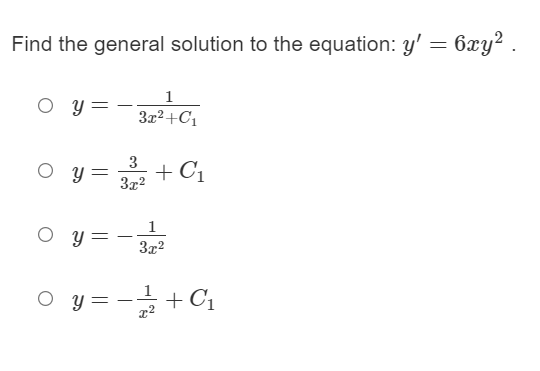









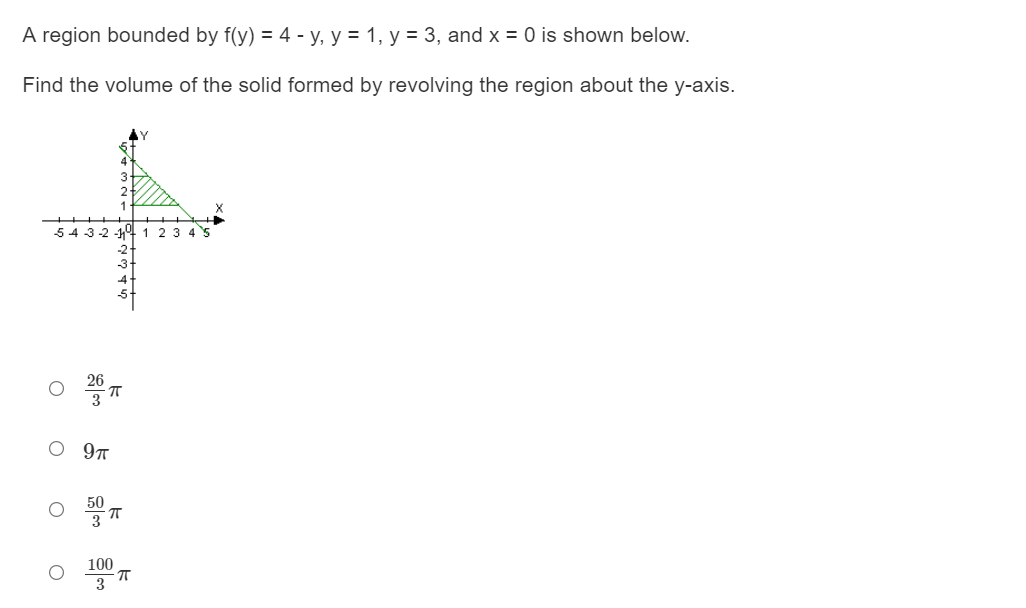





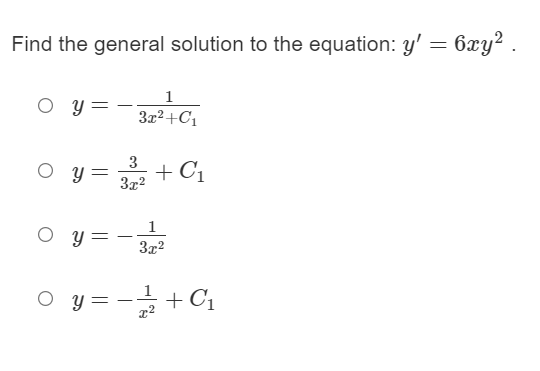





![the Mean Value Theorem apply on the interval [0, 2] and why?](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667782ddb503b_317667782dd9fce1.jpg)

![2]. O The Mean Value Theorem applies because, f(x) is differentiable on](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667782de73347_318667782de61c76.jpg)
A region bounded by f(x) = -x2 + 5, y = 1, and x = O is shown below. Find the volume of the solid formed by revolving the region about the x-axis. 0 27.?33 0 30.133 0 55.46? 0 58.833 A region bounded by y) = 4 - y, y = 1, y = 3, and x = O is shown below. Find the volume of the solid formed by revolving the region about the y-axis. 5432- 1234 -\\2 3 4 5 02:71' 0971' 05;71' Orr Find the volume of the solid formed by revolving the region about the y-axis. Y -NWAGOYO0 X -21 1 234 56 78 O 93 5 TT O 99 O 20T O 36TTA region bounded by y) = -y + 4, y = 1, and x = 1 is shown below. Find the volume of the solid formed by revolving the region about the y-axis. 234 A region bounded by y) = 23: + 2, y = O, y = 3, and x = 1 is shown below. Find the volume of the solid formed by revolving the region about the y-axis. 23456T89 hhhb' O 3611' O 6311' O 242 O 8hr Rewrite the following equation with the variables separated: y' - 4x2 = 3x3. dy O dx = (4+ 3x)202 O dy = (4x2 + 3x3) dx O dy dx = (4ac2 - 3x3) O da = (4x2 + 3x3) dycell Rewrite the following equation with the variables separated: 2y' = O dy 1 2er da O dy ey dx O dy dx 2 O dy 2ey\fGiven the initial condition y(0) = 5, find the particular solution of the equation eyy' 43*: = 0. o y : 111(2312 + 143.413) 0 y : 111(332 + 143.413) 0 y : 111(232 143.413) 0 111(334 + 143.413) Find the equation of the curve that passes through the point (0, 3) and has a slope of 3: at any point (x, y). 0 y : 21:1 |a': + 1| 0 y:2ln|m1|+3 O y :1n|a':| + 3 O y:21n|m+1|+3 For x} 2 \"3:232 does the Mean Value Theorem apply on the interval [0, 2] and why? 0 The Mean Value Theorem applies because f(x) is continuous on [0, 2]. O The Mean Value Theorem applies because, f(x) is differentiable on the closed interval [0, 2]. O The Mean Value Theorem does not apply because f(x} is not continuous on the closed interval [0, 2]. O The Mean Value Theorem does not apply because f(x} is not differentiable on the closed interval [0, 2]. For it) : m2 + 3 |1c|does the Mean Value Theorem apply on the interval [-2, 2] and why? 0 The Mean Value Theorem does not apply because f(x) is not continuous on the closed interval [-2, 2]. O The Mean Value Theorem does not apply because f(x) is not differentiable on the closed interval [-2, 2]. O The Mean Value Theorem applies because f(x) is continuous on [-2, 2]. O The Mean Value Theorem applies because, f(x) is differentiable on the closed interval [-2, 2]. For f(ac) = 2a2 - ac + 1, find all the values of c on the interval [0, 1] that satisfy the Mean Value Theorem. O c= -0.5 O C = 0.375 O c = 0.5 O C = 0.68For f(a) = - Vac + 2, find all the values of c on the interval [2, 7] that satisfy the Mean Value Theorem. O C=-4.75 O C= -4.25 O c = 4.25 O c = 4.75Let f(ac) = a3 - 4xc. Using Rolle's Theorem, what are all the values c in the interval [-2, 2] such that f '(c) = 0? O c= I 2V/3 3 O c= 0.5 and c = -0.5 O c = 12V3 O c = 1 and c = 2Sue is a runner. At time t = 0 she runs down a steep hill, turns around and runs back up it. At time t = 1 she is in the same place she started. Assume that her elevation (let the bottom of the hill be elevation 0), is f(x) = (x - 0.5|, [0, 1]. Can Rolle's Theorem be applied to show that at some point between t = 0 and t = 1, Sue has achieved a maximum and/or minimum speed? O The conditions of Rolle's Theorem are met and Rolle's Theorem does not state that you can find min or max points. O The conditions of Rolle's Theorem are not met but Rolle's Theorem does not state that you can find min or max points. O The conditions of Rolle's Theorem are not met. O The conditions of Rolle's Theorem are met and Rolle's Theorem does state that you can find min or max points
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


