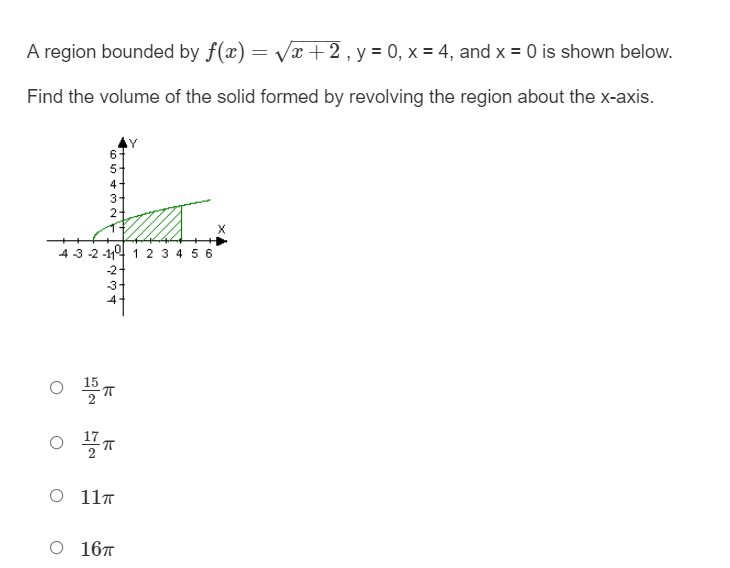
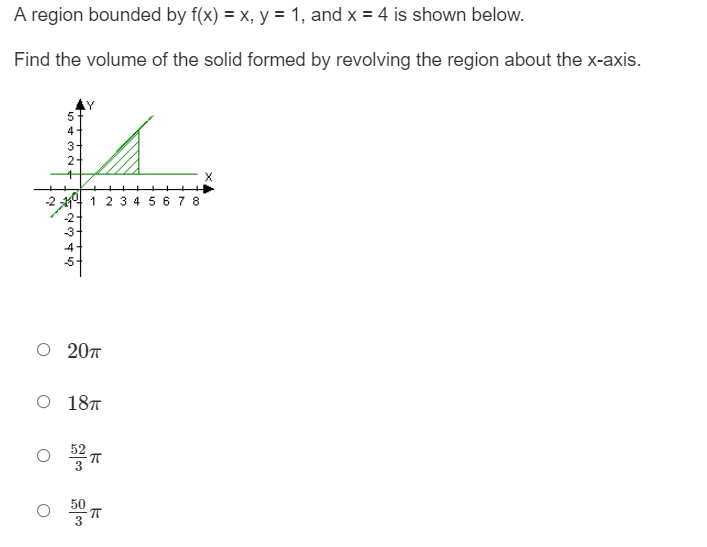
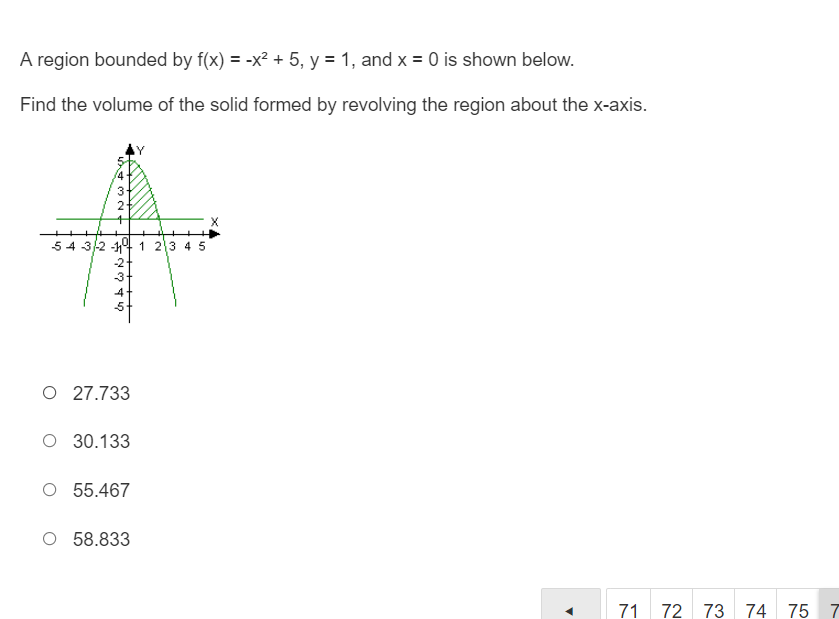
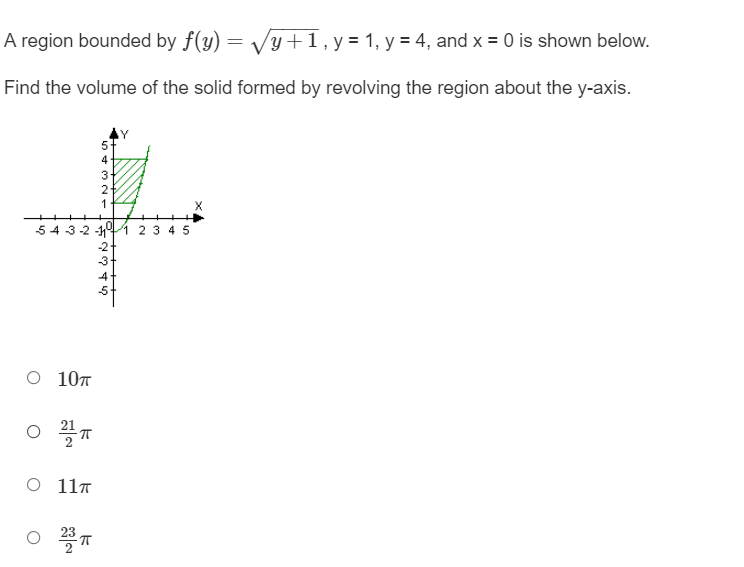
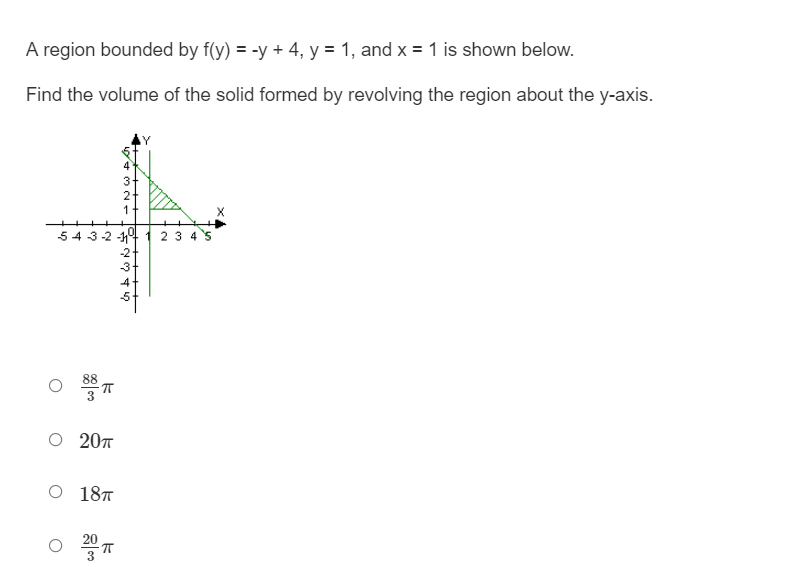
A region bounded by m) = do: I 2 , v = 0,1: = 4, and x = D is shown below. Find the volume of the solid formed by revolving the region about the xsxis. A region bounded by f(x} = x, v = 1, and x = 4 is shown below. Find the volume of the solid formed by revolving the region about the xexis. A region bounded by x} = -x2 + 5, y = 1, and x = U is shown below. Find the volume of the solid formed by revolving the region about the xaxis. 0 27.?33 0 30.133 0 55.46? 0 58.833 4 T172737475? A region bounded by y) 2 y l 1 , v = 1,5! = 4, and x = D is shown below. Find the volume of the solid formed by revolving the region about the v-exis. 5 4 3 2 1 11" -2 3 .4 -5 A region bounded by y) 2 {3/37 , v = 1, v = 8, and x = D is shown below. Find the volume of the solid formed by revolving the region about the vaxis. mmhmmwmm 4 T3 T4 T5 A region bounded by ftv} = -v + 4, v = 1, and x = 1 is shown below. Find the volume of the solid formed by revolving the region about the vaxis. 4 3 2 1 543.241" 23 4 -2 5 .4 45 A region bounded by y} = y: + 3. v = U, y = 2, and x = '1 is shown below. Find the volume of the solid formed by revolving the region about the yaxis. O 39w 0 120.637 0 38w 0 192 5 \fRewrite the following equation with the variables separated: y' = y-7 0 7dy = (y - 7) xdx O dy 7 ac y-7 o dy = 7edx (y-7) O (y -7) dy = 7xdxFind the general solution to the equation: y' = ysin(2x + 3) . O y = In cos(21+3) 2 + C1 DOG(24 3) O y = e 2 O y = C'ecos(21+3) cos(21 1 3) O y = Ce 2Find the equation of the curve that passes through the point (0, 2) and has a slope of 3: at any point (x, y). 0 Sizing2 O y=x3+2 O y=2x3+4