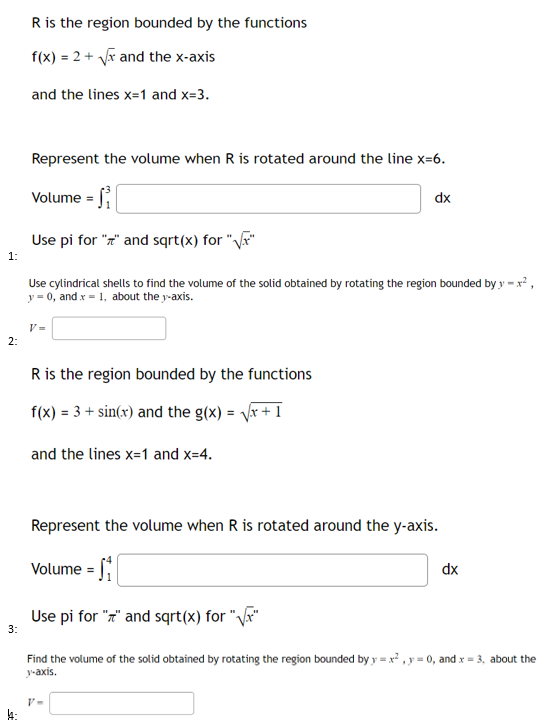
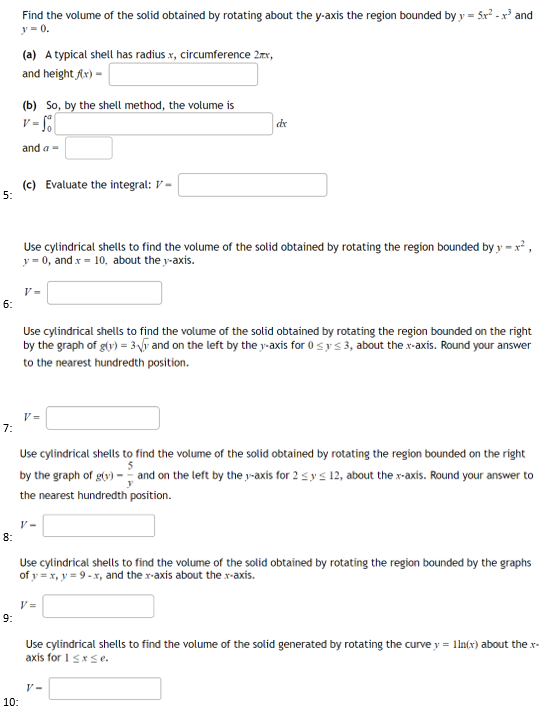
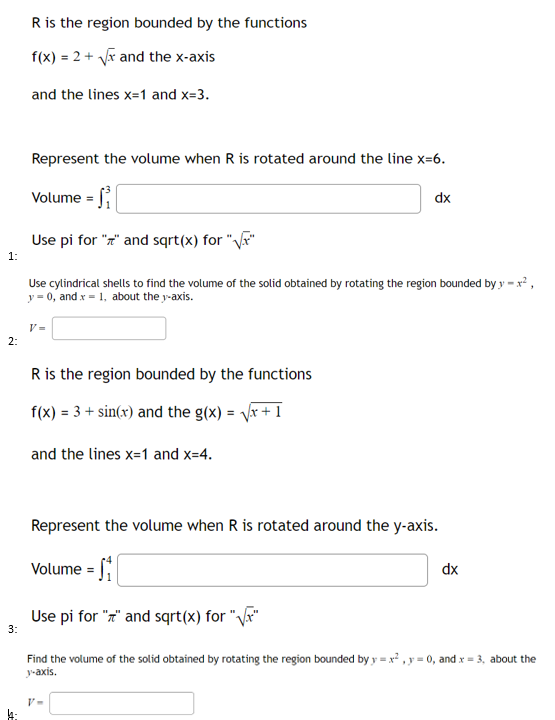
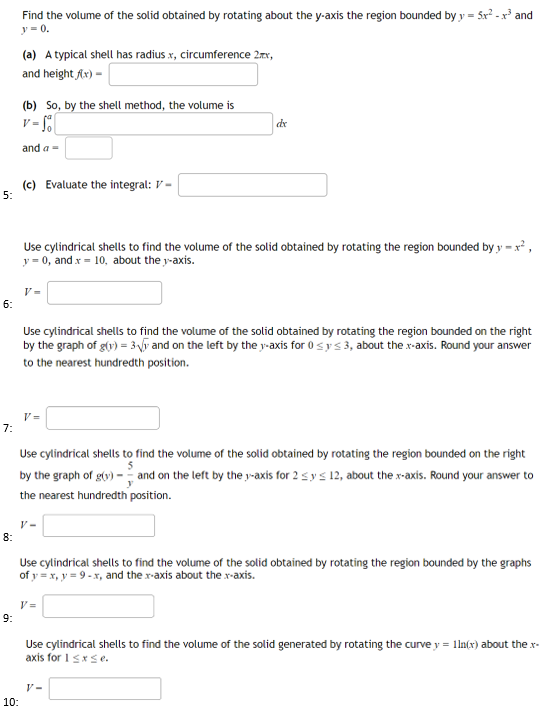
R is the region bounded by the functions f(x) = 2 + vx and the x-axis and the lines x=1 and x=3. Represent the volume when R is rotated around the line x=6. Volume = fi dx Use pi for "" and sqrt(x) for "x" 1: Use cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y = x2 , y = 0, and x = 1, about the y-axis. V = 2- R is the region bounded by the functions f(x) = 3 + sin(x) and the g(x) = Vx + 1 and the lines x=1 and x=4. Represent the volume when R is rotated around the y-axis. Volume = 1 dx Use pi for "I" and sqrt(x) for " (x" 3: Find the volume of the solid obtained by rotating the region bounded by y = x , y = 0, and x = 3. about the Yaxis.Find the volume of the solid obtained by rotating about the y-axis the region bounded by y = 5x -x and V = 0. (a) A typical shell has radius .x, circumference 2xx, and height fix) = (b) So, by the shell method, the volume is V = So dx and a = (c) Evaluate the integral: V - 5: Use cylindrical shells to find the volume of the solid obtained by rotating the region bounded by y = x , 1 = 0, and x = 10, about the y-axis. 6 Use cylindrical shells to find the volume of the solid obtained by rotating the region bounded on the right by the graph of g(y) = 3 /y and on the left by the y-axis for 0 sys 3, about the x-axis. Round your answer to the nearest hundredth position. 7: Use cylindrical shells to find the volume of the solid obtained by rotating the region bounded on the right by the graph of g(y) - - and on the left by the y-axis for 2 sys 12, about the x-axis. Round your answer to the nearest hundredth position. V = 8- Use cylindrical shells to find the volume of the solid obtained by rotating the region bounded by the graphs of y= x, y= 9 -x, and the x-axis about the x-axis. 9: Use cylindrical shells to find the volume of the solid generated by rotating the curve y = IIn(x) about the x- axis for I sx se. 10