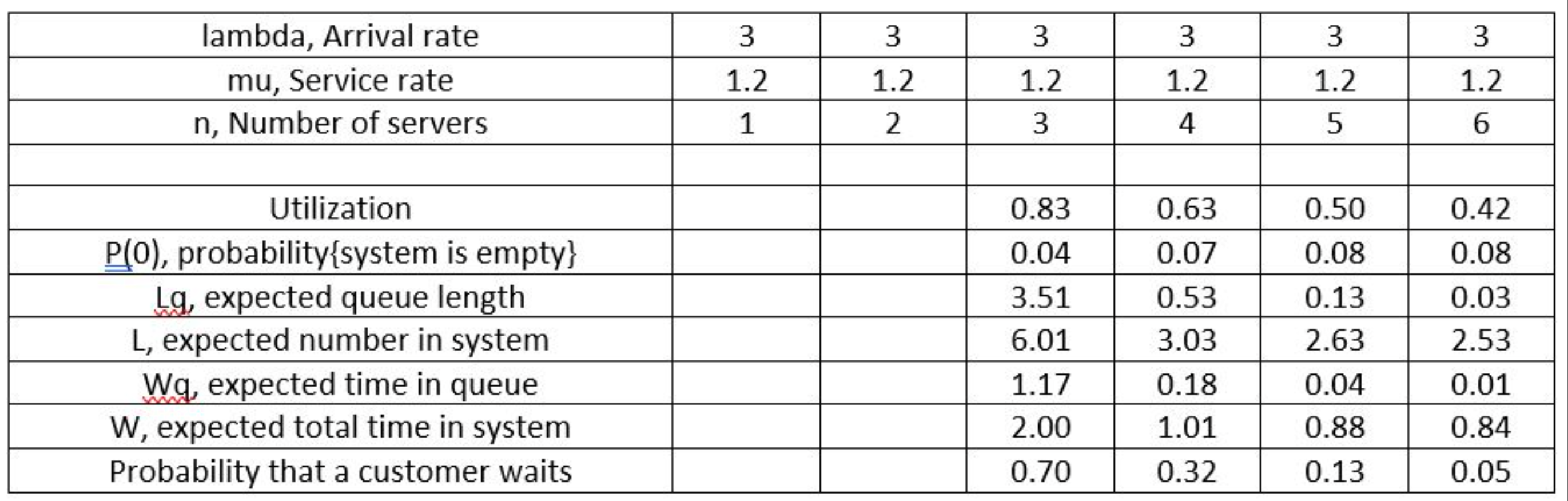
A shipping company operates a docking facility. On average, 3 ships arrive to unload their cargoes per hour. A team of workers unloads each ship. Each team costs $25 / hour. On average, each team can unload 6 ships in 5 hours. The firm pays an hourly charge of $10 per ship for the delay. How many teams are necessary at minimum in order to avoid creating a huge congestion (infinitely long waiting time) of ships in a docking facility and to guarantee a stable operation of the system? (I am asking you to find the minimum number of servers that satisfies the utilization is less than 1.)

a) at least 1

b) at least 2

c) at least 3

d) at least 4

e) at least 5

3 3 3 3 3 3 lambda, Arrival rate mu, Service rate n, Number of servers 1.2 1.2 1.2 1.2 1.2 1.2 1 2 3 4 5 6 0.83 0.63 0.50 0.42 0.04 0.07 0.08 0.08 3.51 0.53 0.03 Utilization PCO), probability{system is empty} Lg, expected queue length L, expected number in system Wq, expected time in queue W, expected total time in system Probability that a customer waits 0.13 2.63 6.01 3.03 2.53 0.18 0.04 1.17 2.00 0.01 0.84 1.01 0.88 0.70 0.32 0.13 0.05