Question: A simple graph is called self-complementary if it is isomorphic to its complement. Let G be a self-complementary graph. 1 v v 4 [a] Prove

A simple graph is called self-complementary if it is isomorphic to its complement. Let G be a self-complementary graph.

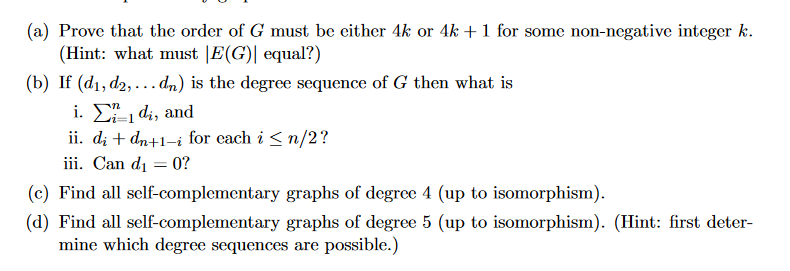
1 v v 4 [a] Prove that the erder of G must be either 4!; er 4!: + 1 for seme nonnegative integer k. (Hint: what must |E[G]| equal?) (13) If {(11, d2, . . . (in) is the degree sequence of G then what is i. 2;; d5, and ii. d.- + dn+1_1- fer eaeh i E nf2? iii. Can d1 = e? [c] Find all selfeemplementarj,r graphs of degree 4 (up to isomorphism). [d] Find all selfeemplementsry graphs ef degree 5 (up to isomorphism). (Hint: rst deter mine which degree sequenees are possible.)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Assume graphs are simple and undirected We say a graph G is self-complementary if G is isomorphic to its complement G. Explain why no graph having only two or three vertices can be self-complementary...

Problem 1 : In class, we saw that trees have several important properties. But what might surprise you is that many of these properties serve as an equivalent definition of a tree! In this problem,...

With this set of problems, we will develop algorithms for All - Pairs Shortest Paths ( APSP ) in graphs. PROBLEM: ( APSP ) . Given a graph G = ( V , E ) with w : E R that gives a real weight to every...

2. If the simple graph G has n vertices and m edges, how many edges does G have? 3. Suppose that graph G is isomorphic to graph G. Show that if G contains a cycle of length k so does G'. 4. Prove...

(a) A sequence d_1, d_2, d_n of integers is called graphic if there is a simple graph G on n vertices, such that the values d_1, d_n are the degrees of the n vertices of G. For example, the sequence...

(a) Let G be an undirected graph with n vertices. If G is isomorphic to its own complement , how many edges must G have? (Such a graph is called self-complementary.) (b) Find an example of a...

A graph G is called self-complementary if it isomorphic to its complement G. For a self-complementary graph G = (V, E), let |V| = n, then (a) find | E|, and (b) prove that G is connected

(a) Let G = (V, E) be a loop-free undirected graph. Recall that G is called self-complementary if G and are isomorphic. If G is self-complementary (i) determine |E| if |V| = n; (ii) prove that G is...

The distance de(u, v) of two vertices in a graph G = (V, E) is defined to be the length of a shortest path connecting u and v if they belong to the same component of G and otherwise. The diameter of...

need typed answer do anyone your wish dont provide code need algorithm 2. A dominating set of a graph is a subset D of vertices such that every vertex that is not in D is adjacent to some vertex in...

What information should a department store gather before adding a new watch brand to its product mix?

Carolyn Luttrell owns Just the Right Thing, a small antiques shop with four employees. For one payroll period the total withholding tax for all employees was $1,633. The total employees' Social...

Use the example of Trident Company described in the notes. The company has 1 million Pound receivable. They are comparing the hedging result of each hedging tool. According this graph, indicate ( 1 )...

Nikoto Steel Co. budgeted manufacturing costs for 50,000 tons of steel are: Fixed manufacturing costs $50,000 per month Variable manufacturing costs $12.00 per ton of steel Nikoto produced 40,000...