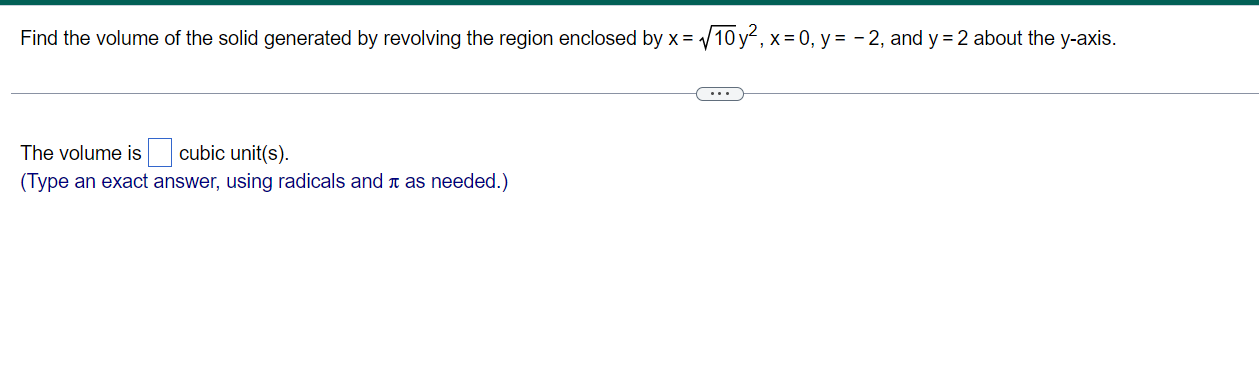
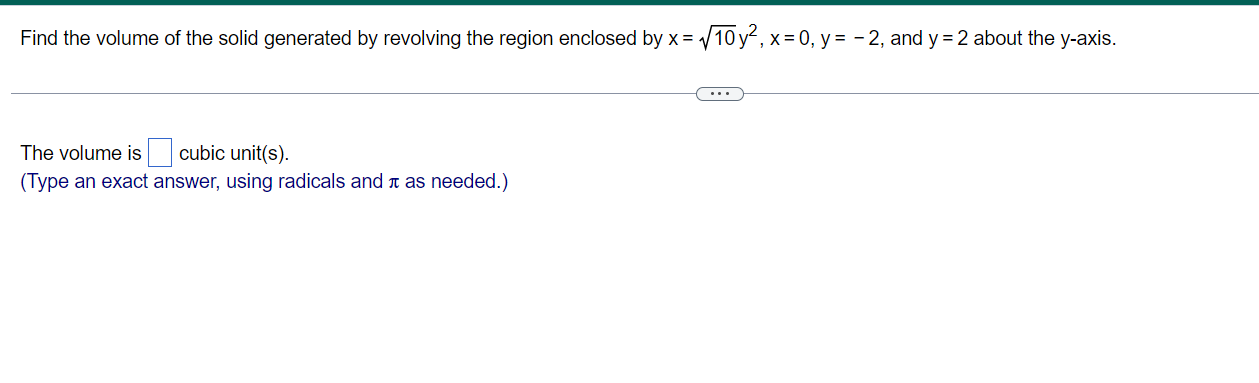
A solid lies between planes perpendicular to the xaxis at X: 0 and x = 12. The cross-sections perpendicular to the axis on the interval 0 s x s 12 are squares with diagonals that run from the parabola y = 21/; to the parabola y = 21/}. Find the volume of the solid. The volume of the solid is cubic units. (Type an exact answer, using 7: as needed.) Find the volume of the solid generated by revolving the region bounded by y = 2x2, y = 0, and x = 4 about the xaxis. The volume of the solid generated by revolving the region bounded by y = 2x2, y = 0, and x = 4 about the x-axis is cubic units. (Type an exact answer, using It as needed.) Find the volume of the solid generated by revolving the region bounded by the given line and curve about the x-axis. y = v16-x , y=0 .. . The volume of the solid is . (Type an exact answer, using it as needed.)Find the volume of the solid generated by revolving the region enclosed by x = @312, x = 0, y = 2, and y = 2 about the y-axis. The volume is cubic unit{s}. (Type an exact answer, using radicals and 1: as needed.) Find the volume of the solid generated by revolving the region bounded by the given curve and lines about the x-axie. y=24,y=4,x=0 V = (Type an exact answer, using at as needed.)