Question: CAN I GET HELP? CALCULUS 221 A solid lies between planes perpendicular to the xaxis at x = 2 and x = 2. The crosssections
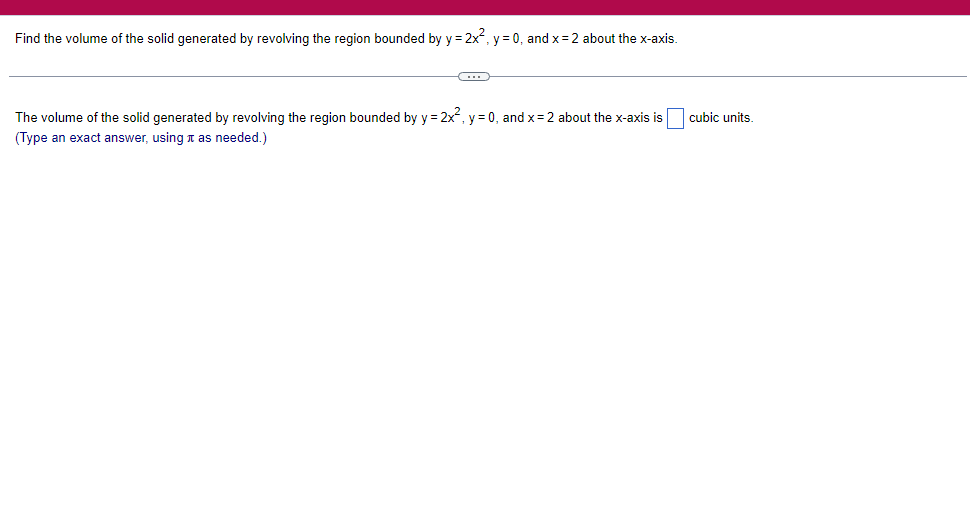


![y = l], and x=2 about the xaxis. (I) The volume of](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679c3a9471e1_9776679c3a935d4c.jpg)





![curve and lines about the 1,raxis. Er 1Iiy+1 x: ,x=i],1,r=i],1,r=3 V: '1](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6679c3aed4143_9826679c3aec0b79.jpg)
CAN I GET HELP? CALCULUS 221
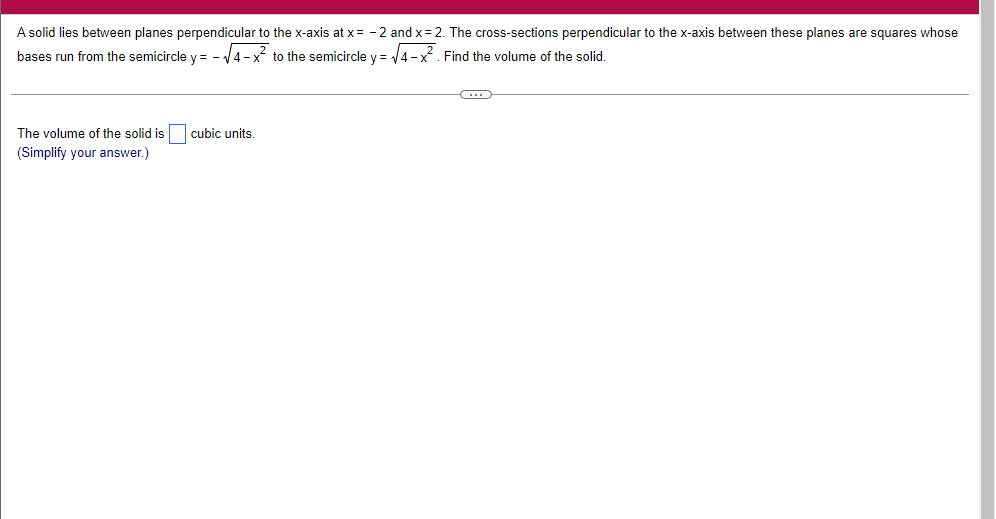
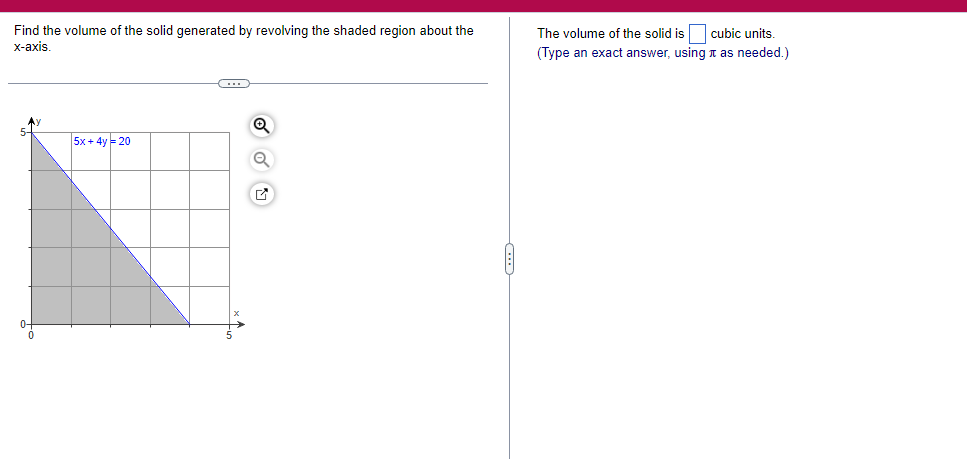
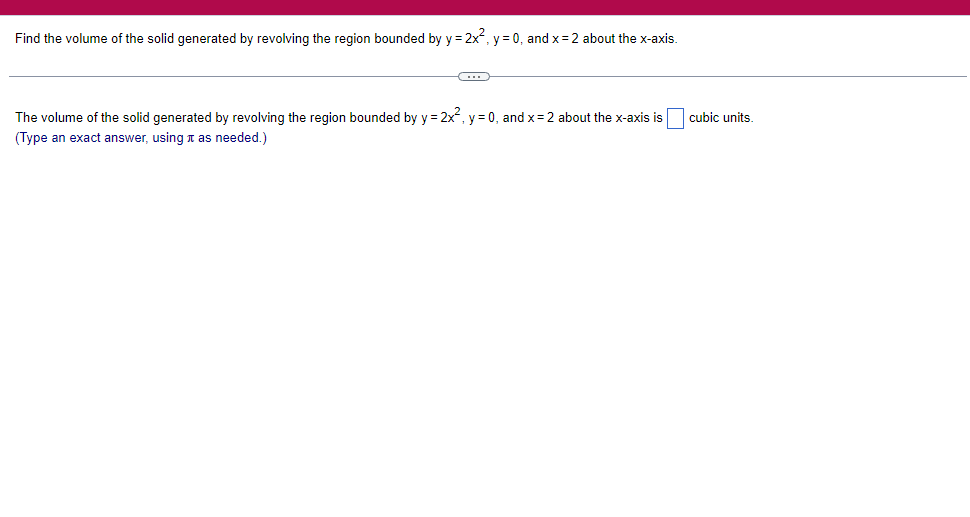

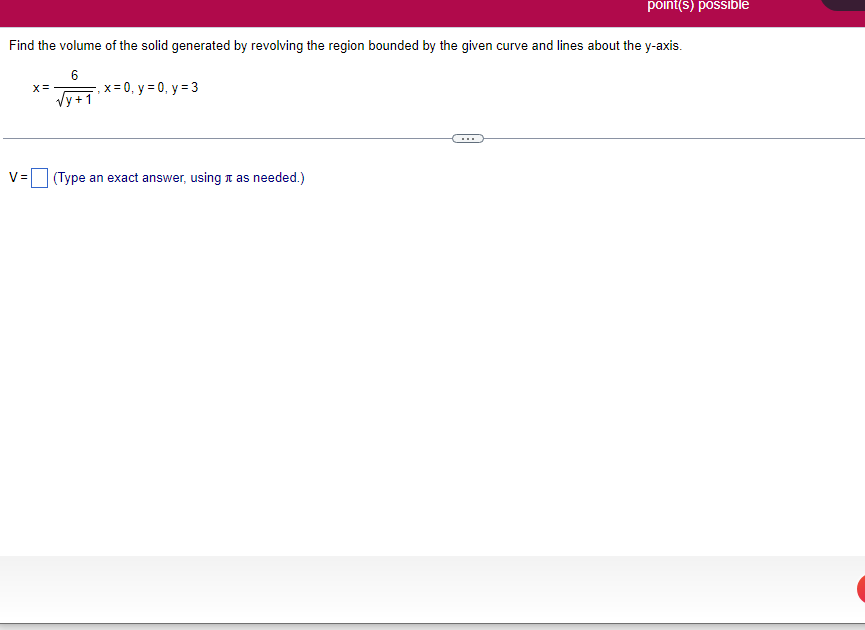
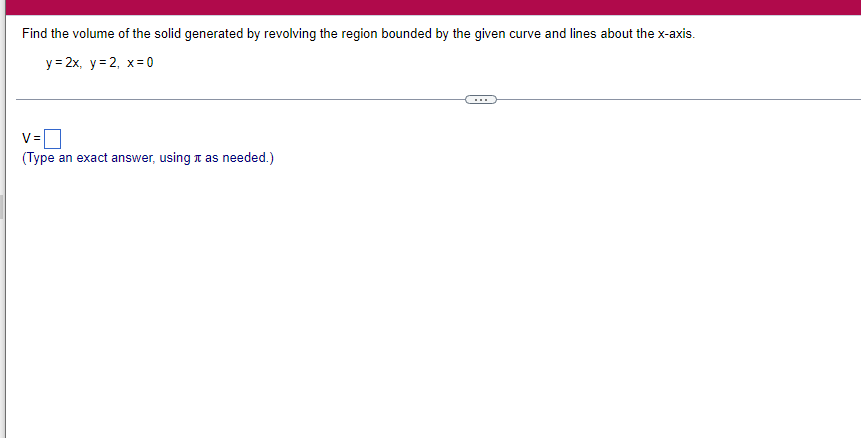
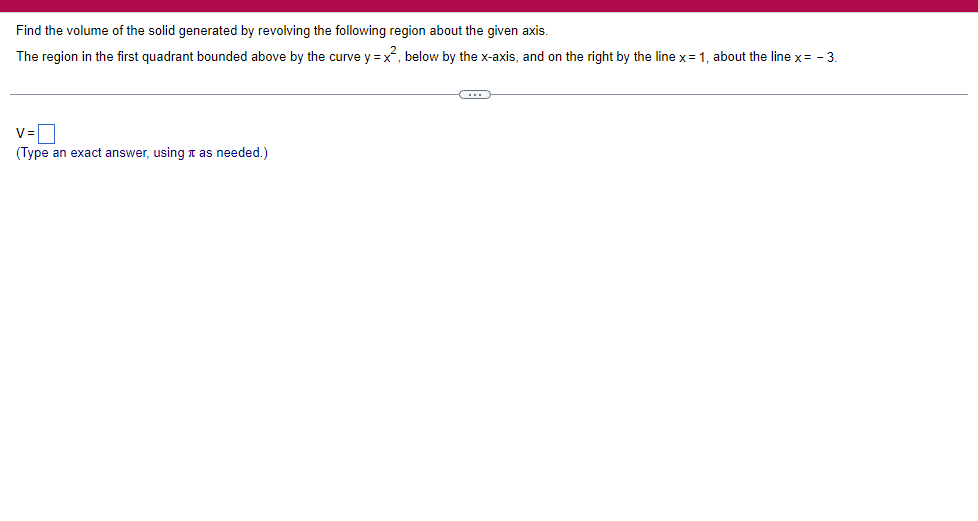
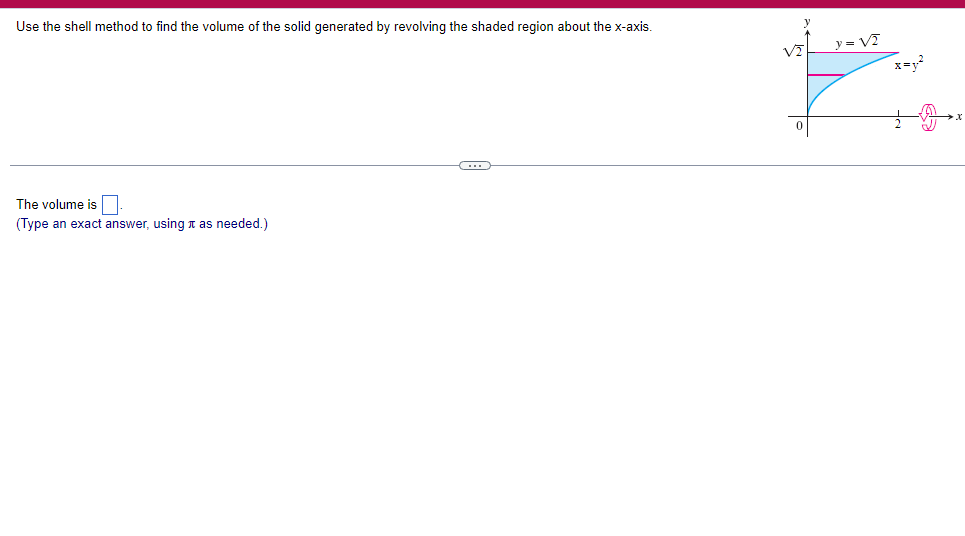

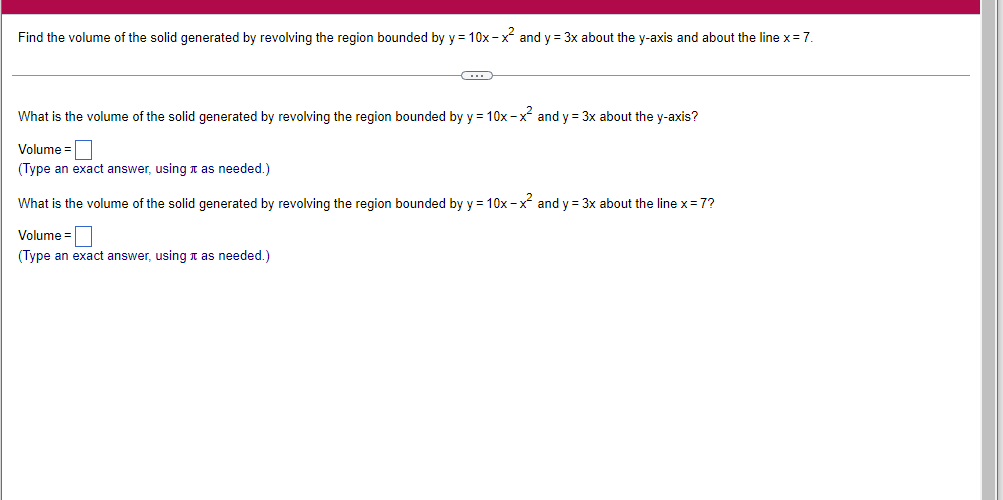
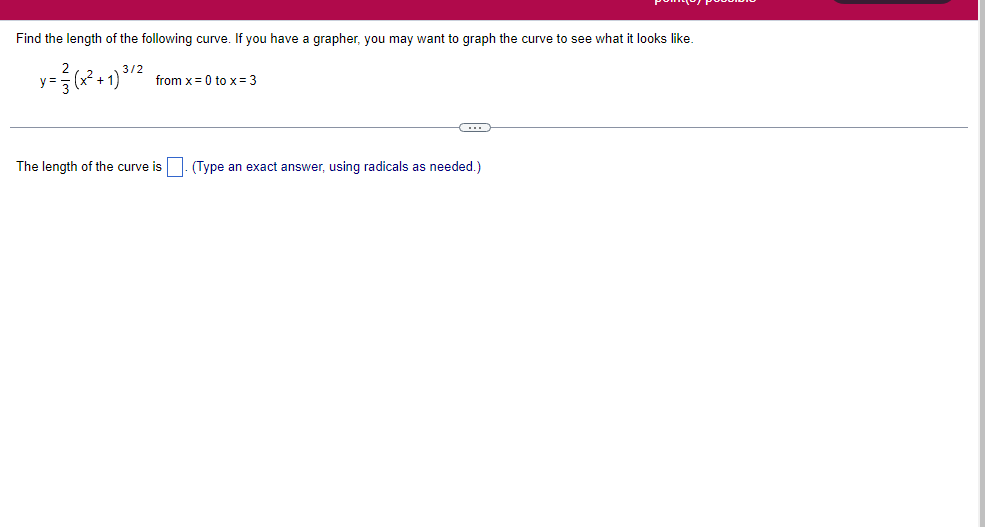
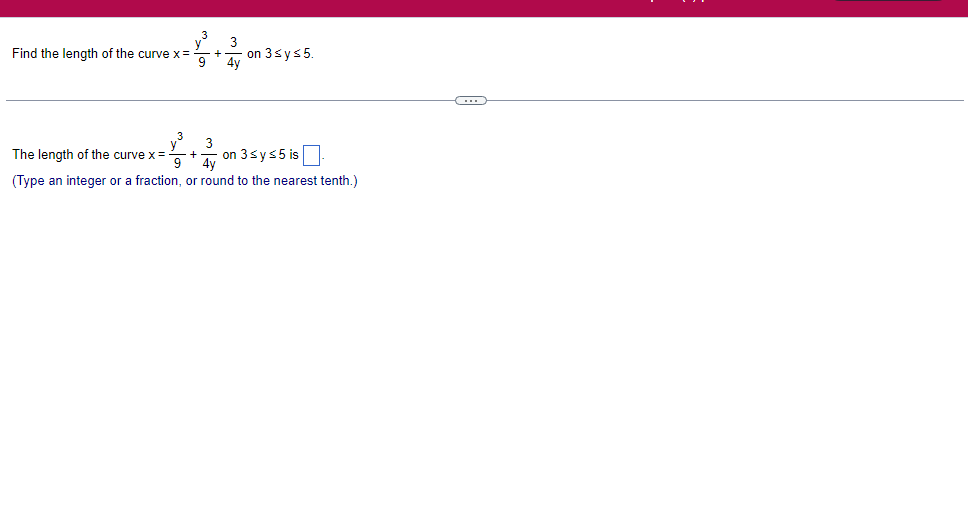
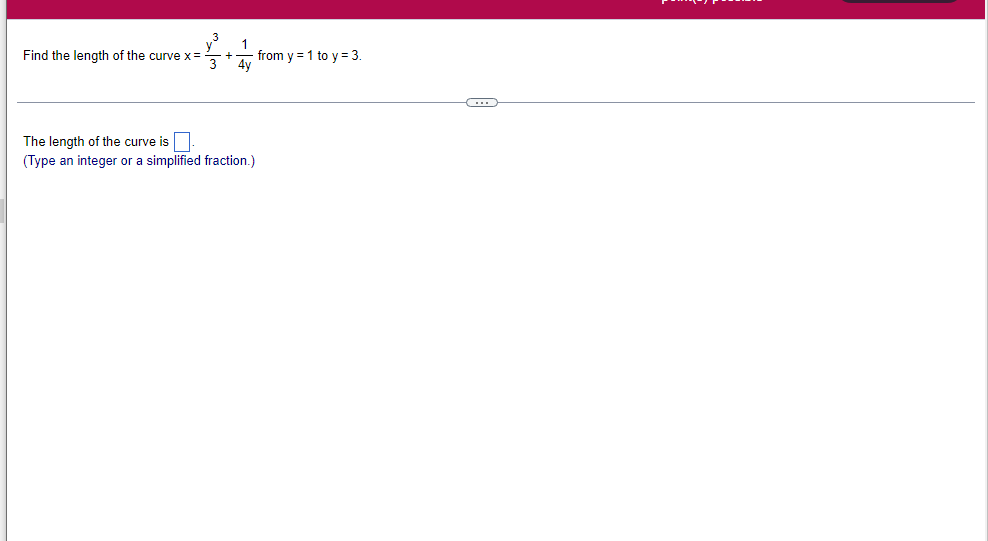



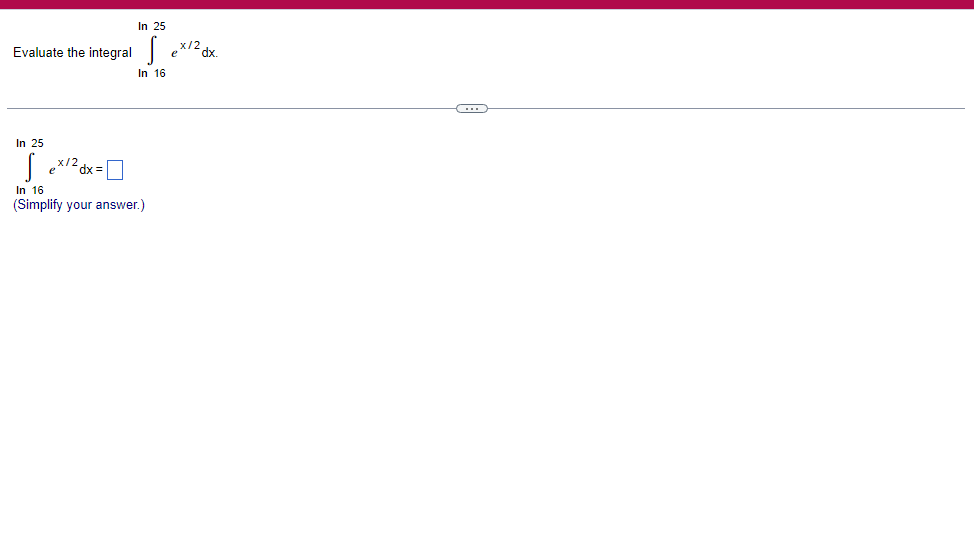
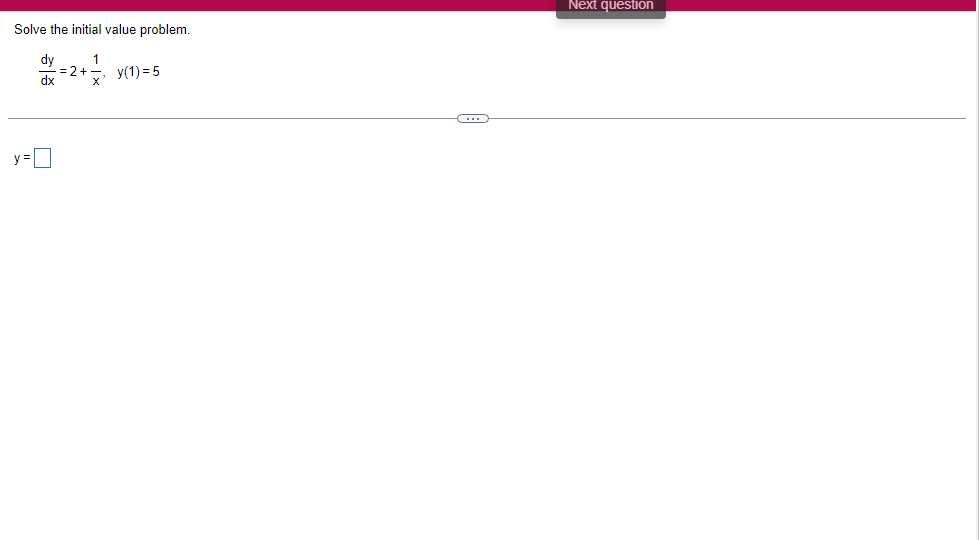
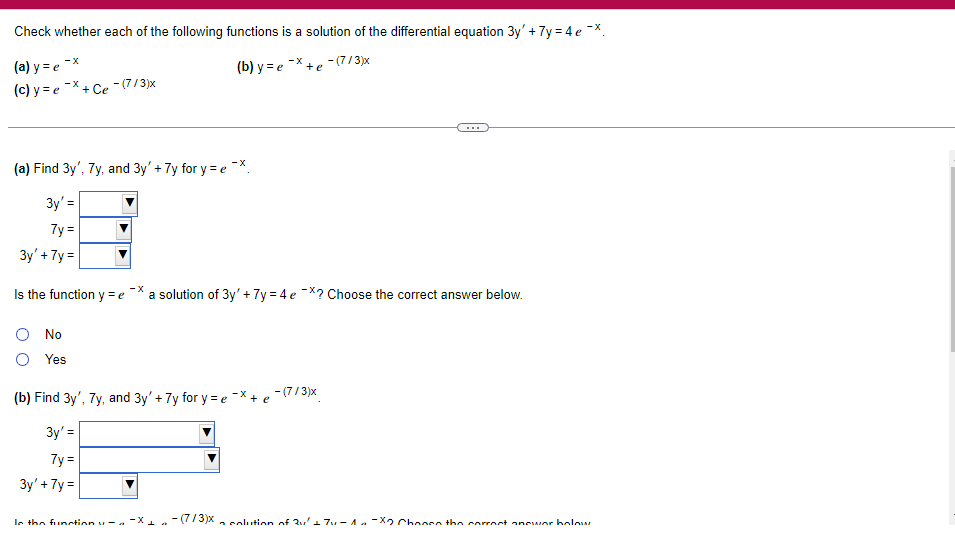


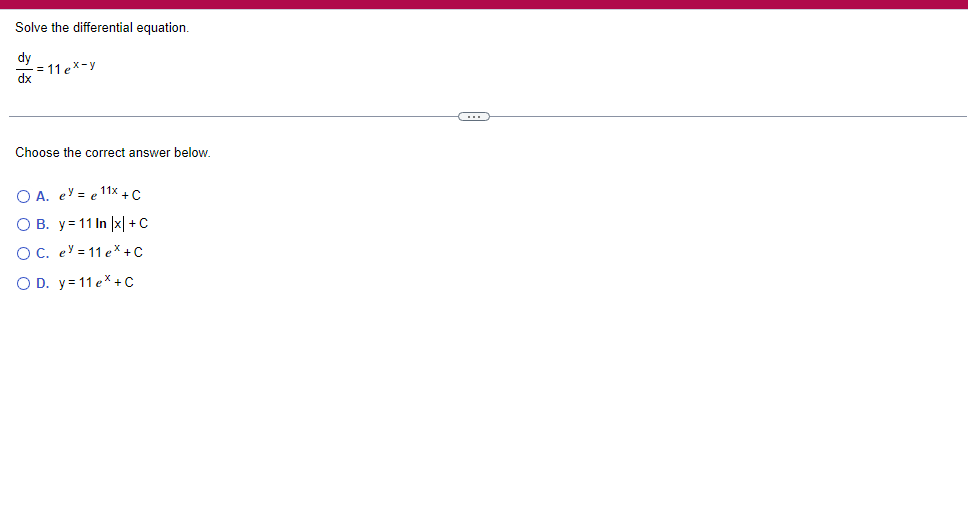
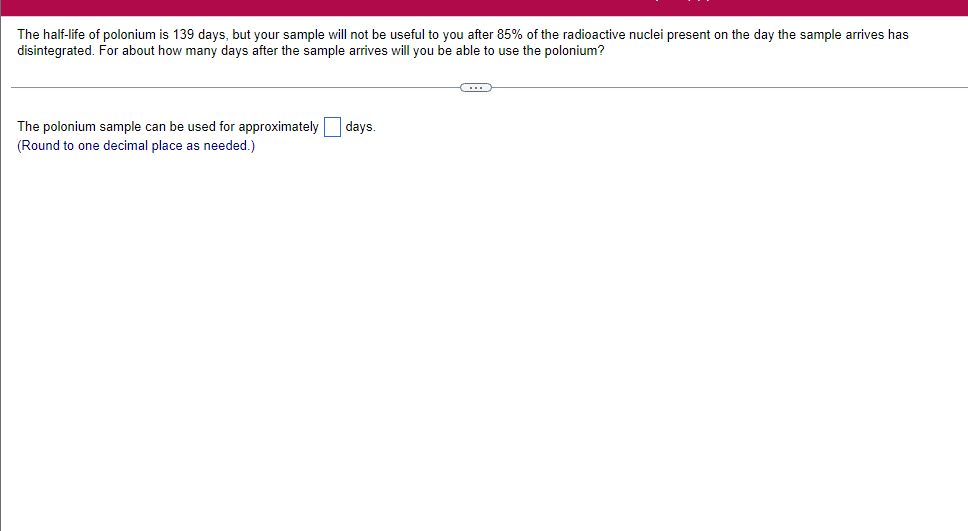
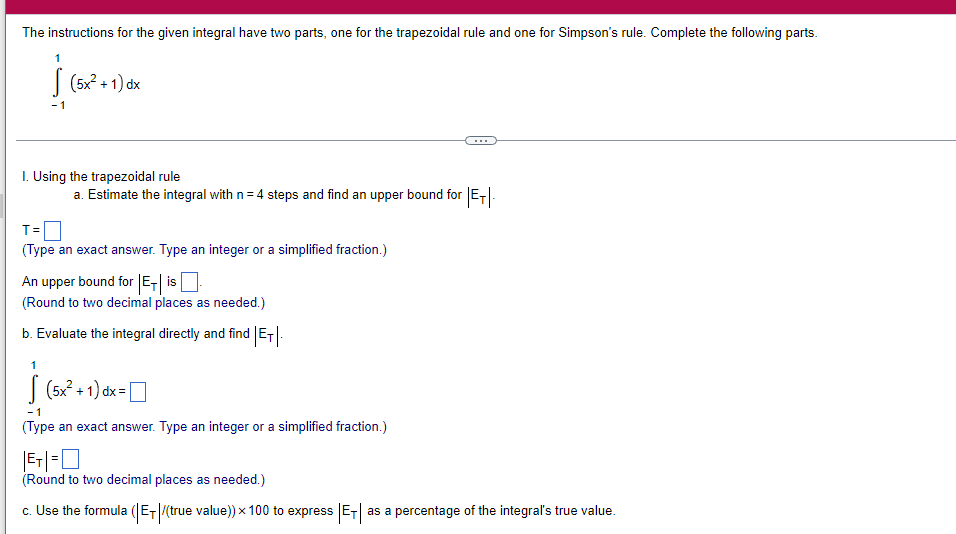
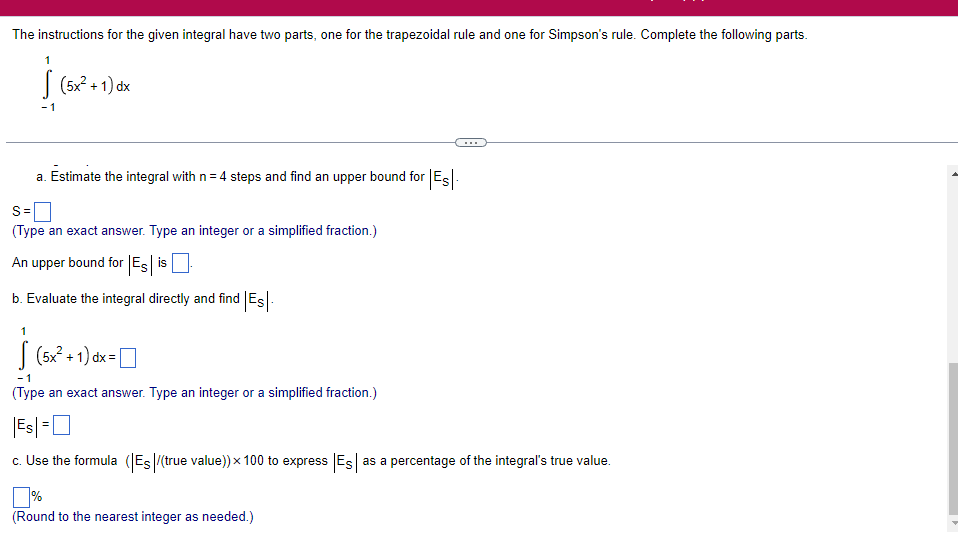
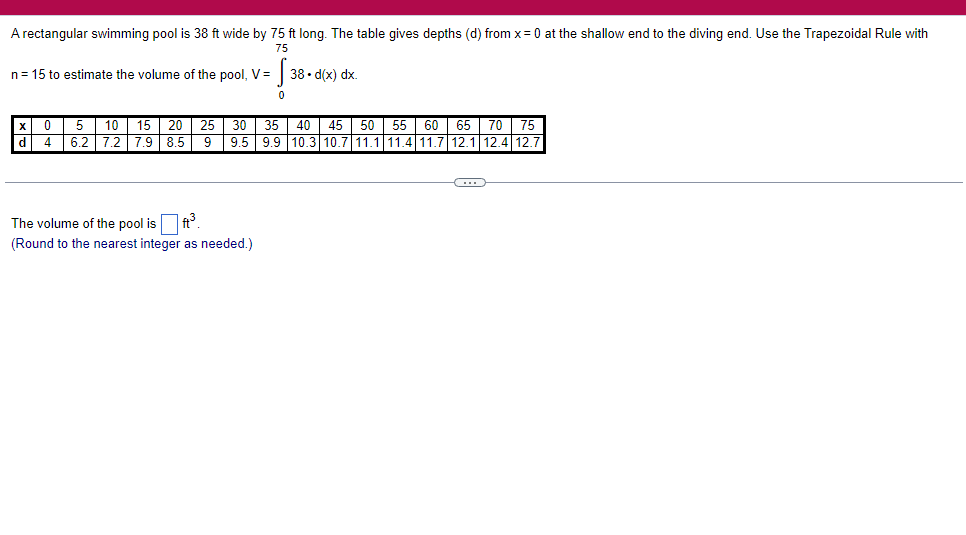
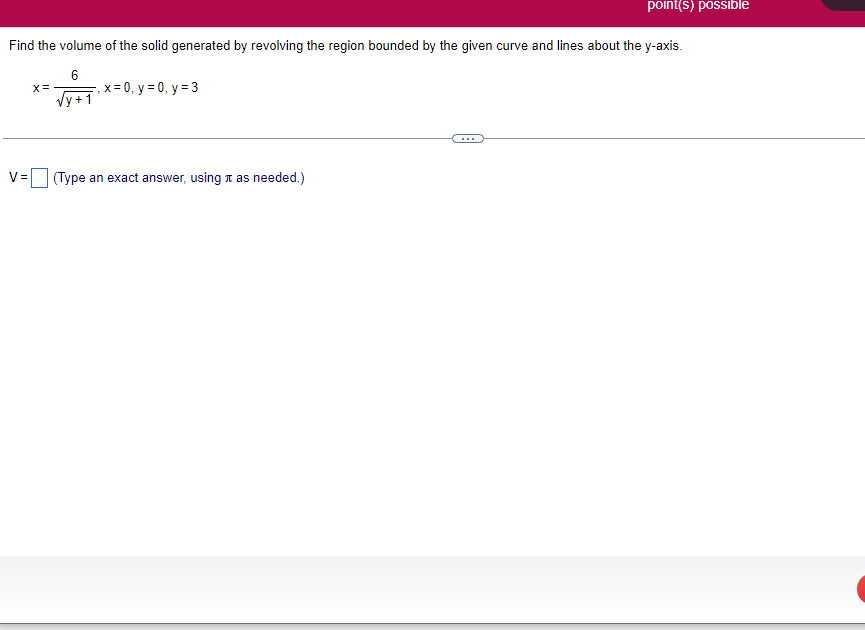
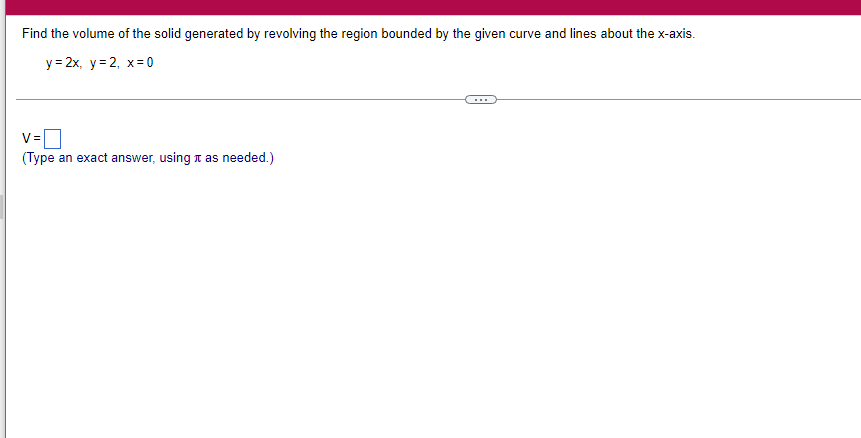
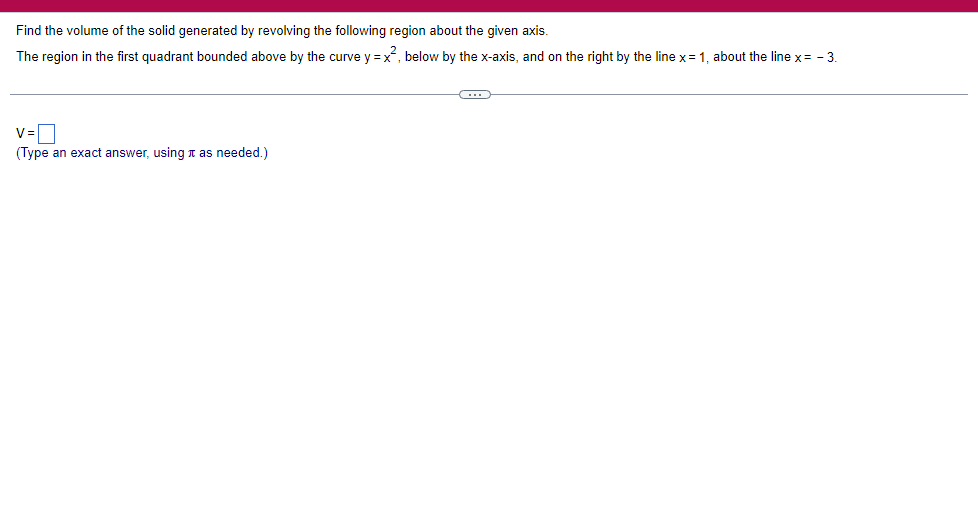
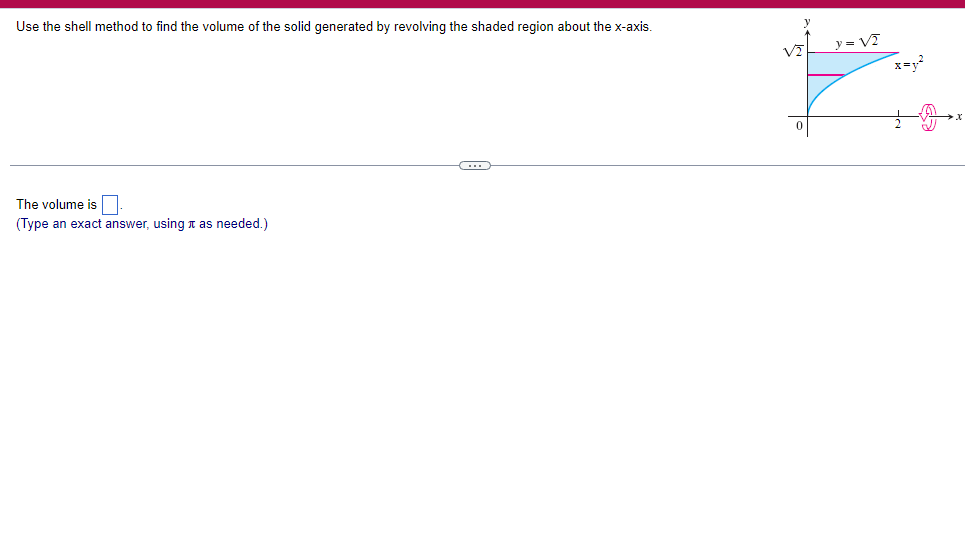
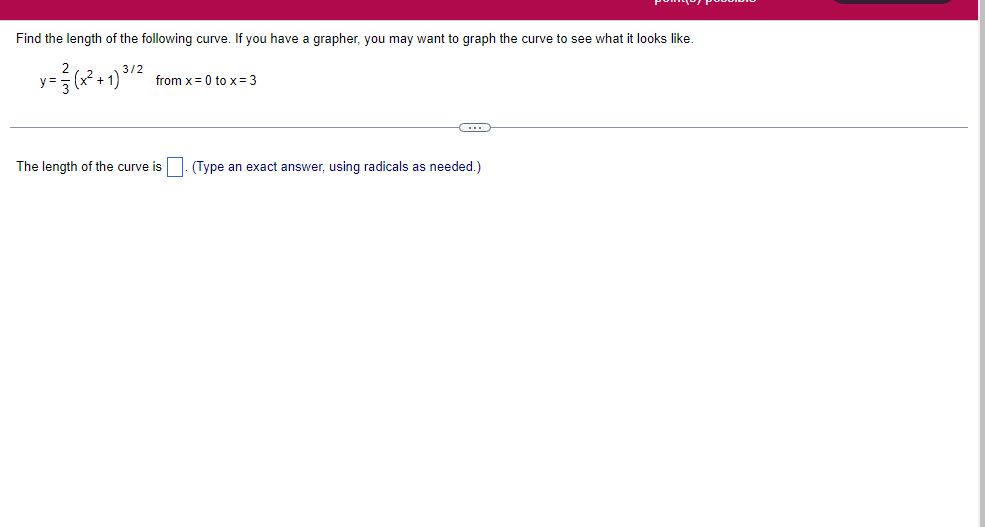
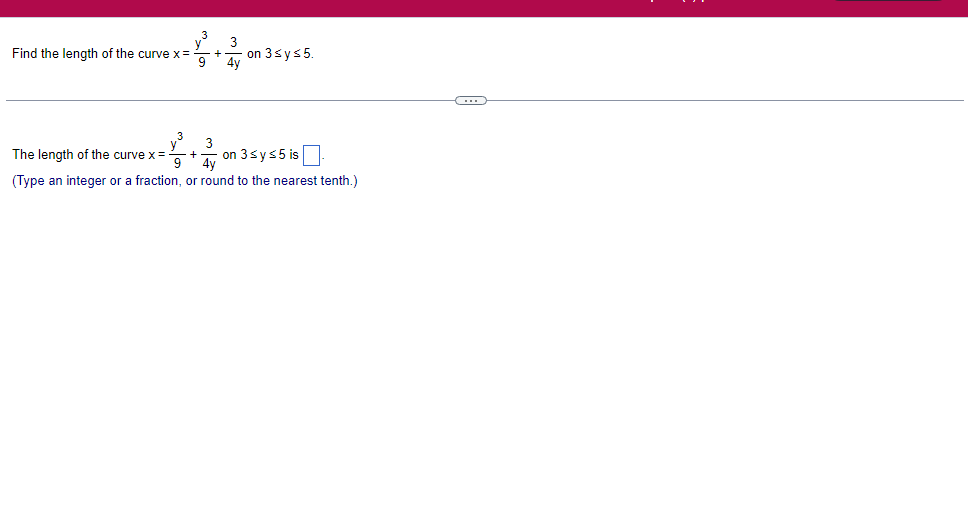
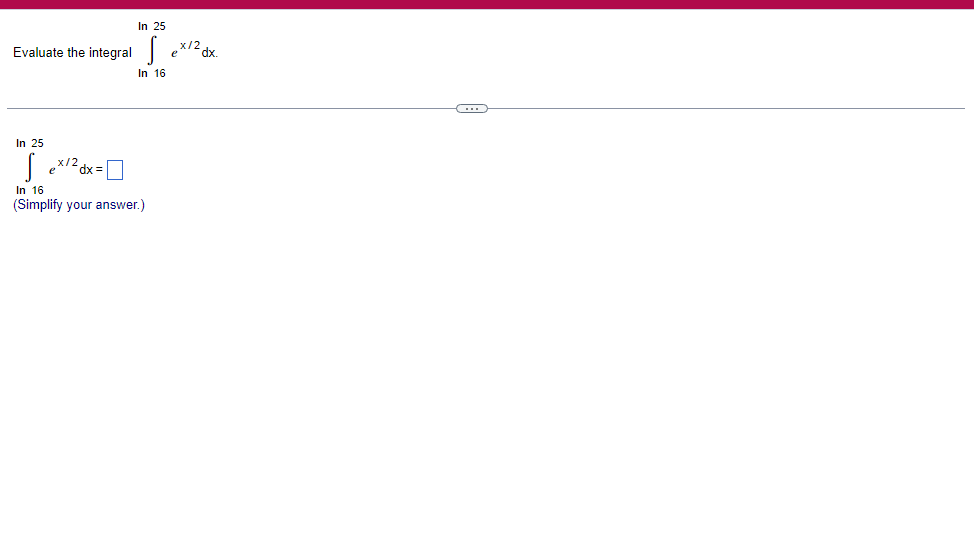
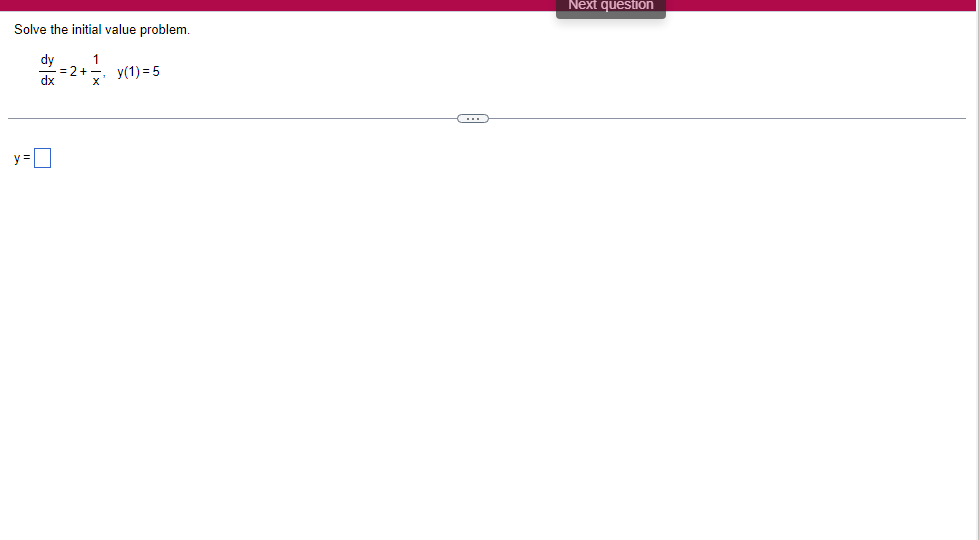
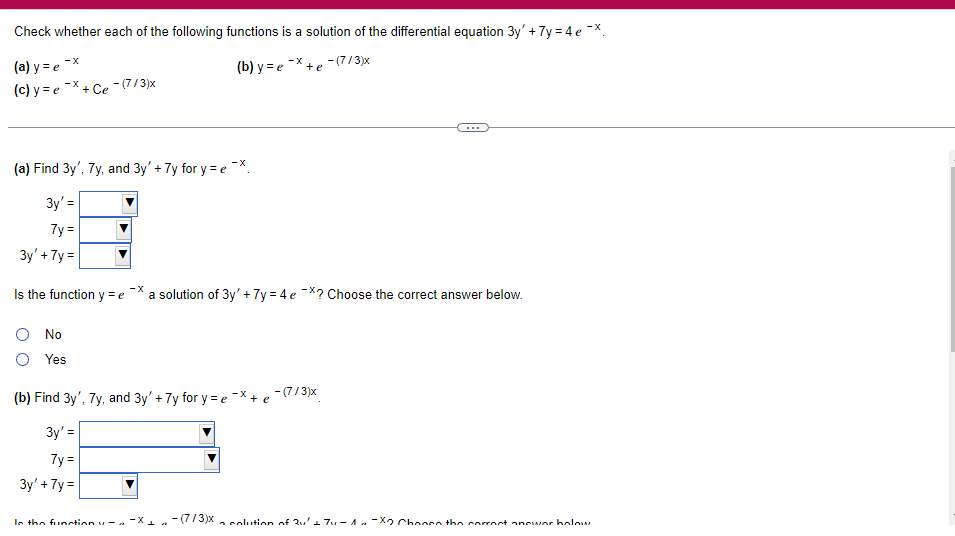
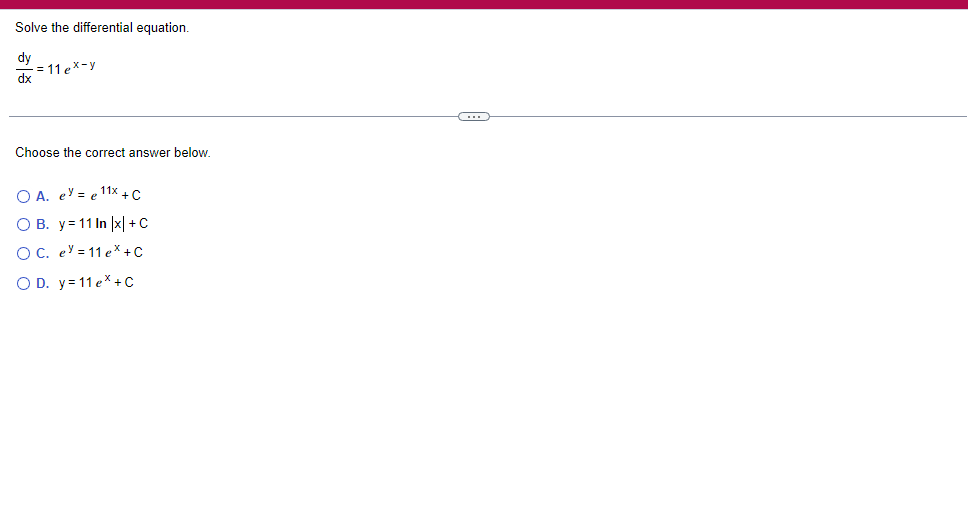
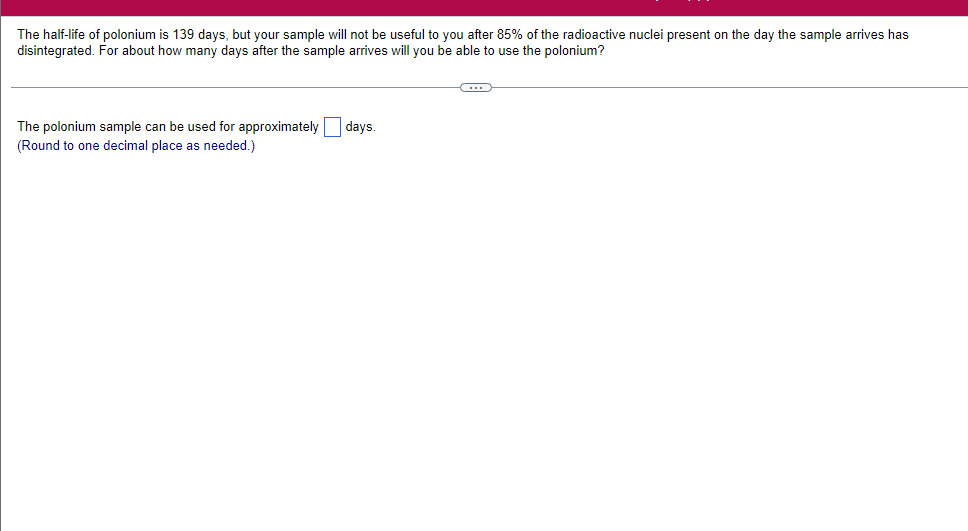
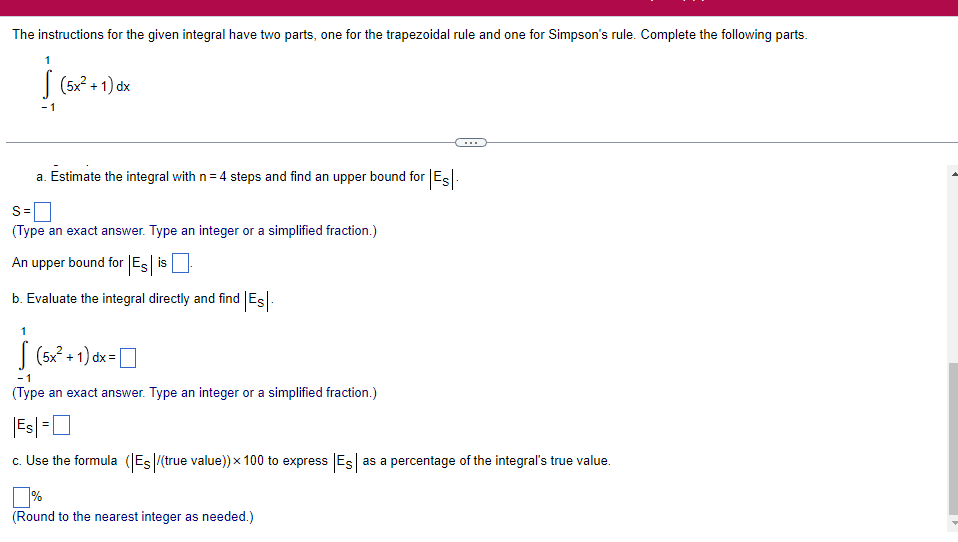
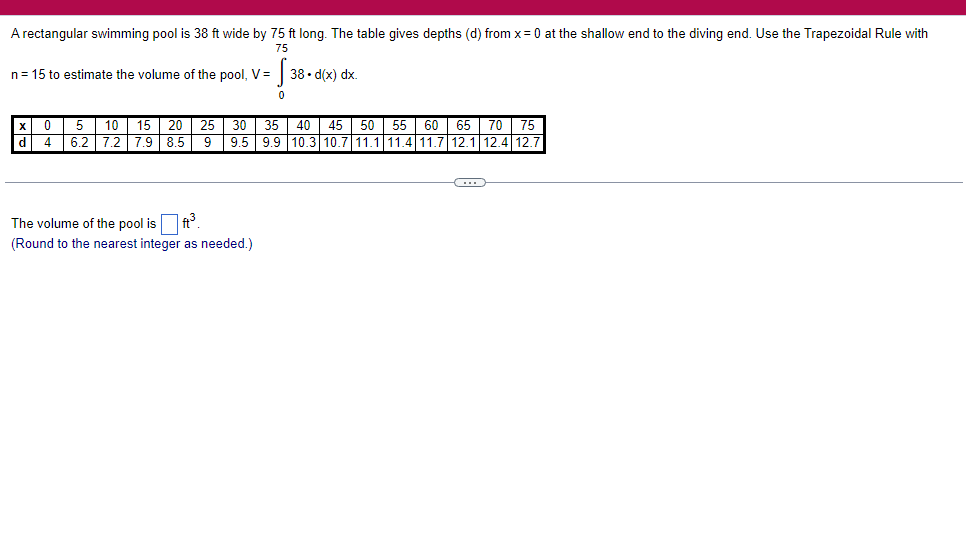
A solid lies between planes perpendicular to the xaxis at x = 2 and x = 2. The crosssections perpendicular to the xaxis between these planes are squares whose bases run from the semicircle y: 1i 4 -x2 to the semicircle y: 4 x2. Find the volume of the solid. The volume oi the solid is D cubic units. (Simplify your answer.) Find the volume of the solid generated by revolving the shaded region about the The volume of the solid is cubic units. X-axis. (Type an exact answer, using it as needed.) 5- 5x + 4y = 20 un-Find the volume of the solid generated by revolving the region bounded by y=2x2, y = l], and x=2 about the xaxis. (I) The volume of the solid generated by revolving the region bounded by y = 2x2, 5r: 0, and x=2 about the xaxis is cubic units. (Type an exact answer, using 1: as needed.) 1: 21': Find the volume of the solid generated by revolving the region bounded by v=4q}' sin 1. 5': [Land x1 = and x2 = about the xaxis. 4 3 I: 2: The volume of the solid generated by revolving the region bounded by y = tlyisin x, v = {Land x1 = I and x2 = 7 about the xaxis is D cubic units. (Round to the nearest hundredth.) pom LS. poser n e Find Ihe volume of the solid generated by revolving The region bounded by The given curve and lines about the 1,raxis. Er 1Iiy+1 x: ,x=i],1,r=i],1,r=3 V: '1 (Type an exacl answer, using 1: as needed.) Find the volume of the solid generated by revolving the region bounded by the given curve and lines about the x-axis. y = 2x, y = 2, x=0 V= (Type an exact answer, using It as needed.)Find the volume of the eolid generated by revolving the following region about the given axis. The region in the rst quadrant bounded above by the curve 3; =x2. below by the xaxis, and on the right by the line x: 1, about the line x: 3. V : (Type an exact answer, using 1: as needed.) Use the shell method to nd the volume of the solid generated by revolving the shaded region about the xaxis. The volume is E. (Type an exact answer, using 11 as needed.) Use the shell method to nd the volume of the solid generated by revolving the shaded region about the yaxis. The volume is |:. (Type an exact answer, using 11: as needed.) Find the volume ofthe solid generated by revolving the region bounded by y=1l1x - x2 and y = 3:: about the yaxis and about the line it = TI". What is the volume of the solid generated by revolving the region bounded by y =1x -x2 and y = 3): about the yaxis'? Volume = (Type an exact answer, using It as needed.) What is the volume of the solid generated by revolving the region bounded by y =1Dx x2 and y = 3): about the line x = 1'? Volume = E (Type an exact answer, using a: as needed.) Find the length of the following curve. If you have a grapher, you may want to graph the curve to see what it looks like. y = W/ N (x2+1) 3/2 from x = 0 to x = 3 The length of the curve is . (Type an exact answer, using radicals as needed.)3 Find the length of the curve x = on 3 sy $ 5. 4y 3 The length of the curve x = + 9 4y on 3 sy $5 is (Type an integer or a fraction, or round to the nearest tenth.)Find the length of the curve x = 3 + from y = 1 to y = 3. Ay The length of the curve is (Type an integer or a simplified fraction.)\fCheck whether each of the following functions is a solution of the differential equation 3y' + 7y =4e -x. (a)y=ex (b)yzexte - (7/3)x (c) y=ex + Ce - (7/3)x (a) Find 3y', 7y, and 3y' + 7y for y = e -x. 3y 7y = 3y' + 7y = Is the function y =e * * a solution of 3y' + 7y =4 e -*? Choose the correct answer below. O No O Yes (b) Find 3y', 7y, and 3y' + 7y for y= e -X + p -(7/3)x 3y' = 7y = 3y' + 7y =\fThe halflite oi polonium is 139 days, but your sample will not be useful to you after 85% of the radioactive nuclei present on the day the sample arrives has disintegrated. For about how many days after the sample anives will you be able to use the polonium? The polonium sample can be used for approximately I: days. (Round to one decimal place as needed.) The instructions for the given integral have two parts, one for the trapezoidal rule and one for Simpson's rule. Complete the following parts. (5x2 + 1) dx -1 I. Using the trapezoidal rule a. Estimate the integral with n = 4 steps and find an upper bound for ET. T = (Type an exact answer. Type an integer or a simplified fraction.) An upper bound for | Et| is- (Round to two decimal places as needed.) b. Evaluate the integral directly and find | ET). 1 ( 5x 2 + 1 ) OX = 1 (Type an exact answer. Type an integer or a simplified fraction.) (Round to two decimal places as needed.) c. Use the formula ( ET /(true value)) x 100 to express ET| as a percentage of the integral's true value.The instructions for the given integral have two parts, one for the trapezoidal rule and one for Simpson's rule. Complete the following parts. (5x2 + 1) dx - 1 a. Estimate the integral with n = 4 steps and find an upper bound for | Es. S =0 (Type an exact answer. Type an integer or a simplified fraction.) An upper bound for |Es | is b. Evaluate the integral directly and find | Es). (5x2 + 1 ) dx = [ -1 (Type an exact answer. Type an integer or a simplified fraction.) |Es| =0 c. Use the formula ( Es /(true value)) x 100 to express |Es | as a percentage of the integral's true value. 7% [Round to the nearest integer as needed.)A rectangular swimming pool is 38 ft wide by T5 it long. The table gives depths {d} from x = U at the shallow end to the diving end. Use the Trapezoidal Rule with 15 n = 15 to estimate the volume of the pool, U = J38 - dbl) (hi. I} i] 51!] 15 2!] 25 3|] 35 4|] 45 5!] 55 Bi] 55 TI] T5 4 6.2 ?.2 7.9 3.5 9 9.5 9.91U.31U.711.111.111171211211127 The volume of the pool is R3. (Round to The nearest integer as needed.)
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


