A supermarket has two self-checkout counters (counters for short), namely Counter 1 and Counter 2. The time between arrivals at the self-checkout zone is 1, or 3 minutes according to the probability distribution in Table 2. The time to complete a transaction at a counter follows the distribution shown in Table 3. 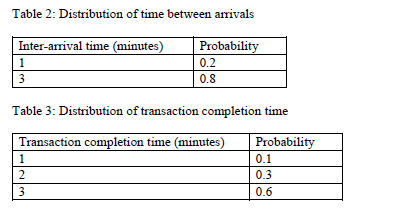When both counters are available, Counter 1 takes the customer. If both are being used, the customer must wait in line; then when a counter is available, the first customer in the line will use that counter to check out. The supermarket wants to study how long a customer stays in the system (= time in the queue + time at a counter). (a) Set up intervals of random numbers that can be used to simulate the inter-arrival time in Table 2, and the transaction completion time in Table 3. (b) Sketch a simulation table and perform a simulation for 3 customers. Assume that, when the simulation begins, both counters are available and the 1st customer will arrive at the self-checkout zone in two minutes. Use the random numbers 0.0745, and 0.1744 to generate simulated values for the inter-arrival time between the 1st and the 2nd customers, and between the 2nd and the 3rd customers, respectively. Use the random numbers 0.6087, 0.6152, and 0.3290 to generate simulated values for the transaction completion time of the 3 customers, respectively. Based on this sample of 3 customers, what is the average time a customer stays in the system?

Table 2: Distribution of time between arrivals Table 3: Distribution of transaction completion time