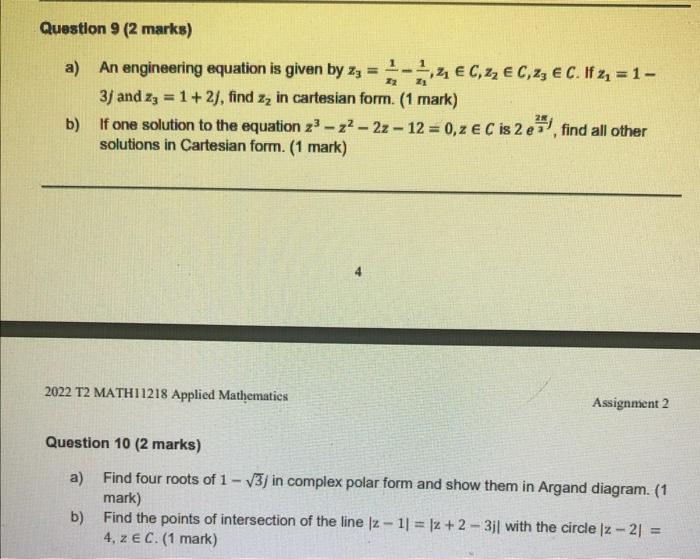
A typical logarithmic function is given by: f(x)=3 log (10) +logz () a) Find the equation for its inverse f(x) and specify its implied domain and range. (1) mark) b) Sketch both f(x) and (x) on the same set of axes showing all important features. What did you notice about these two graphs? (1 mark) [Note1: Recall a sketch does not use technology (e.g., Excel or graphing software) when being generated! So, draw your plot free hand on a graph paper (you can use tools to see the graphs but you need to present hand sketch). This rule applies to all questions requiring sketch] [Note 2: you need to show calculations how you found these features. This rule applies to all questions that require to specify important features on a graph] Question 2 (2 marks) a) Use the exponential definition of sinh(x) and cosh(x) to show cosh (2x) = 2 cosh(x)-1. (1 mark) b) Solve the equation 4 cosh(2x)-2 sinh(x) = 7, giving your answer in terms of natural logarithm (1 mark) Question 3 (2 marks) a) Evaluate and simply: cos s(-x) - cos (+x) b) Find the value of m if cot(20) + tan(0) = m cot(0) Question 4 (2 marks) Solve the following trigonometric equations: a) 2 cos (6)-cos (B)-2 cos(8) +1=0 for-2n SBS 2n b) 2 cosec (30-) == for - 585 2n (1 mark) (1 mark) (1 mark) (1 mark) Question 5 (2 marks) Prove the following trigonometric identities: -b cot(x)=(a+b) sin (x) - b 1+cut (x) =1-sin(20) a) b) Question 6 (2 marks) An engineering function is defined by: sin(0)+cos (0) cos(0)+sin(0) b) f(t)=-2 sin(2t+2)-2cos(2t-2) a) Express the function in the form of f(t) = A cos(at) with 20 (1 mark) b) Express the function in the form of f(t) = A sin(at +) with 0 (1 mark) (1 mark) Question 7 (2 marks) Height of a sea wave is given by h = 5+ 3 cos (-5) where t is time (in hours) after midnight. a) a) b) (1 mark) Question 8 (2 marks) Find the amplitude, angular frequency, frequency, phase angle and time displacement of this trigonometric function. (1 mark) Sketch the graph of one cycle of this wave from 6:00am onwards showing all key features. (1 mark) Show that 1 -/= e in complex number system. Evaluate (5-/)" (4+7) (1 mark) in Cartesian form of the complex number. (1 mark) Question 9 (2 marks) a) An engineering equation is given by z = - 3j and z3 = 1 + 2), find zz in cartesian form. (1 mark) b) If one solution to the equation 2 - 2 - 2z - 12 = 0, z C is 2 e, find all other solutions in Cartesian form. (1 mark) 2022 T2 MATH11218 Applied Mathematics EC,2 C, z, E C. If z = 1- Assignment 2 Question 10 (2 marks) a) Find four roots of 1- 3/ in complex polar form and show them in Argand diagram. (1 mark) b) Find the points of intersection of the line Iz- 1] = [z + 2-3j| with the circle |z-2] = 4, z E C. (1 mark)