(a) What is the optimal solution to this LP problem?

(b) Now suppose that x{1} and x{2} must be integers. What is the optimal solution?

(c) What general principle of integer programming is illustrated by this question?

ANSWER SELECTED ARE WRONG! PLEASE PROVIDE CORRECT ANSWERS THANK YOU.

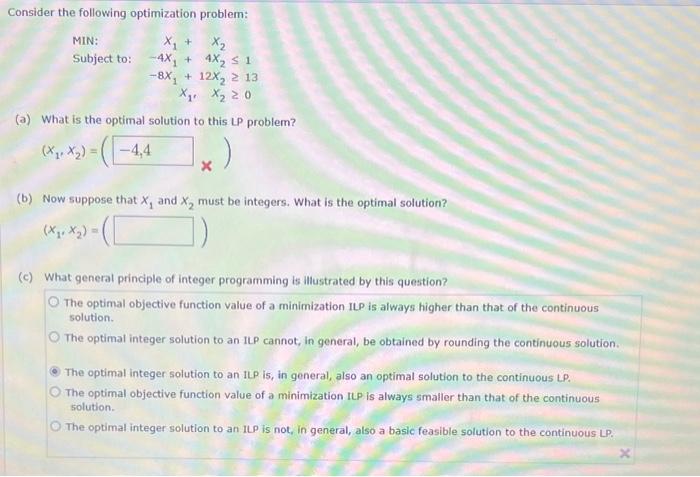
Consider the following optimization problem: MIN:Subjectto:8x1+12x2x1,x1+x24x1+4x213x210 (a) What is the optimal solution to this LP problem? (x1,x2)=(x) (b) Now suppose that x1 and x2 must be integers. What is the optimal solution? (x1,x2)=( (c) What general principle of integer programming is illustrated by this question? The optimal objective function value of a minimization ILP is always higher than that of the continuous solution. The optimal integer solution to an ILP cannot, in general, be obtained by rounding the continuous solution. The optimal integer solution to an ILP is, in general, also an optimal solution to the continuous LP. The optimal objective function value of a minimization ILP is always smaller than that of the continuous solution. The optimal integer solution to an ILP is not, in general, also a basic feasible solution to the continuous LP