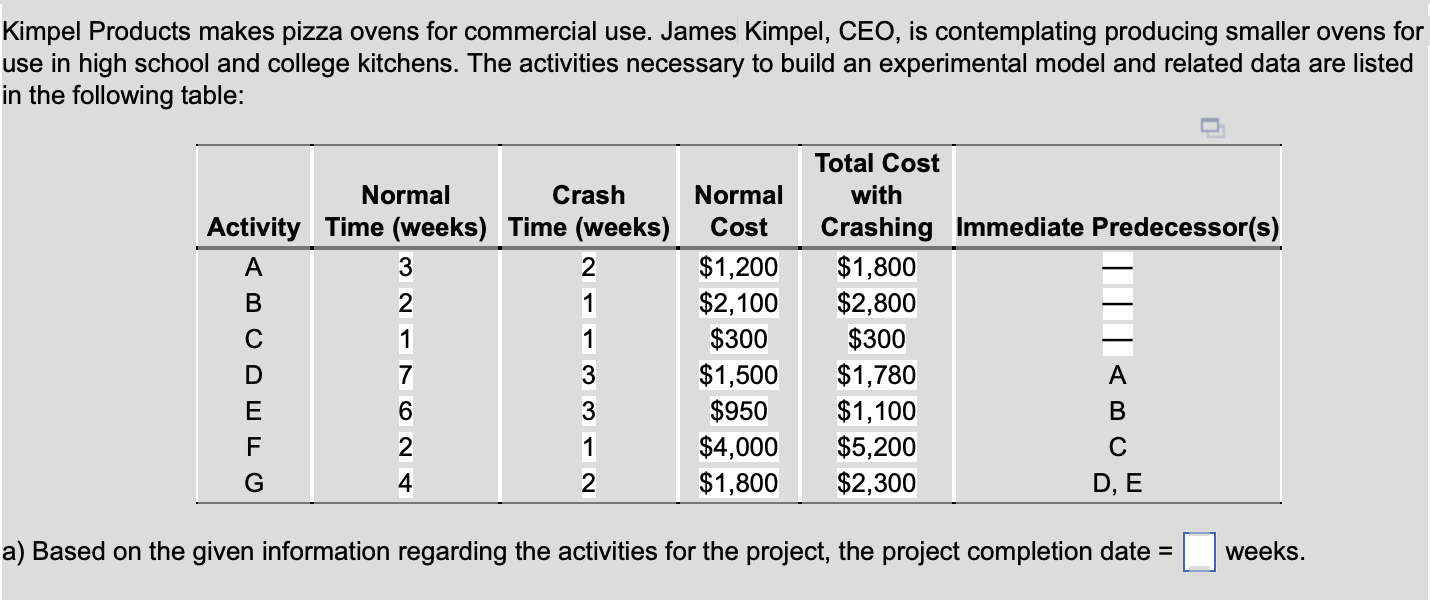
a) What is the project completion date?

The total project completion time corresponds to the longest path through the network.

Part 3

The length of path A

(Enter

your response as a whole

number.)

Part 4

The length of path B

(Enter

your response as a whole

number.)

Part 5

The length of path C - F is

weeks.

(Enter

your response as a whole

number.)

Part 6

Based on the given information regarding the activities for the project, the project completion date =

weeks.

Part 7

b) Crash this project to 10 weeks at the least cost.

Part 8

To speed up the project at the least additional cost, first crash the activity that has the lowest crash cost per day. Determine the crash cost per week for each activity on the critical path.

For activity A, the per week crashing cost =

your response as a whole

number.)

Part 9

For activity D, the per week crashing cost =

=

(Enter

your response as a whole

number.)

Part 10

For activity G, the per week crashing cost =

=

(Enter

your response as a whole

number.)

Part 11

The first activity to crash is

by

2

weeks.

Part 12

The cost of the project based on the first activity selected for crashing will increase by

$140140.

(Enter

your response as a whole

number.)

Part 13

What is(are) the critical path(s) after crashing activity D down to 5 weeks?

A.

Both A - D - G and C - F are critical.

B.

Both A - D - G and B - E - G are critical.

This is the correct answer.

C.

A - D - G is still critical.

D.

B - E - G is critical.

Part 14

Hence, any further crashing must be done to both critical paths.

Part 15

Determine the crash cost per day for activities on path B - E - G.

For activity B, the per day crashing cost =

$750750.

(Enter

your response as a whole

number.)

Part 16

For activity E, the per day crashing cost =

=

(Enter

your response as a whole number.)

Part 17

For activity G, the per day crashing cost is

$250.

Part 18

On each of these critical paths, identify one activity that can still be crashed. Also the total cost of crashing the project should be the smallest. Therefore, one should crash activity D and activity

E

by

2

weeks for an additional total cost of

$340340.

(Enter

your response as a whole number.)

Part 19

c) Crash this project to 7 weeks (which is the maximum it can be crashed) at the least cost.

Part 20

Both A - D - G and B - E - G are still critical.

Part 21

Activity D cannot be crashed any further, since it has reached its crash limit of

3

weeks.

Note that activity

G

is common to both paths. That is, by crashing this activity, we will simultaneously reduce the completion time of both paths, which yields the smallest total cost.

Part 22

Therefore, one should crash activity G by 22

weeks for an additional total cost of_________

Next, one should crash activity

and activity E by

1

week for an additional total cost of

$

(Enter

your response as a whole number.)

Part 24

Total cost of crashing the project to 7 weeks is calculated as

=

$enter your response here.

(Enter

your response as a whole number.)

Kimpel Products makes pizza ovens for commercial use. James Kimpel, CEO, is contemplating producing smaller ovens use in high school and college kitchens. The activities necessary to build an experimental model and related data are list in the following table: a) Based on the given information regarding the activities for the project, the project completion date = weeks