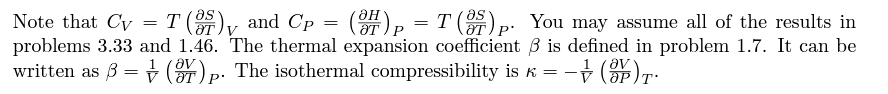
(a) With the heat capacity expressions from Problem 3.33 in mind, first con- sider S to be a function of 7 and V. Expand dS in terms of the partial derivatives (05/87) v and (05/OV)r. Note that one of these derivatives is related to Cv. (b) To bring in Cp, consider V to be a function of T and P and expand dV in terms of partial derivatives in a similar way. Plug this expression for dV into the result of part (a), then set dP =0 and note that you have derived a nontrivial expression for (25/87) p. This derivative is related to Cp, so you now have a formula for the difference Cp-Cv. (c) Write the remaining partial derivatives in terms of measurable quantities using a Maxwell relation and the result of Problem 1.46. Your final result should be TV3- Cp = Cv + KT (d) Check that this formula gives the correct value of Cp - Cv for an ideal (e) Use this formula to argue that Cp cannot be less than Cy.Problem 3.33. Use the thermodynamic identity to derive the heat capacity formula CV =T which is occasionally more convenient than the more familiar expression in terms of U. Then derive a similar formula for Up, by first writing d// in terms of dS and dP.Note that Cv = T (or ) and Cp = OH (or ) p. You may assume all of the results in problems 3.33 and 1.46. The thermal expansion coefficient 8 is defined in problem 1.7. It can be written as 3 = 1 OV . The isothermal compressibility is K = -v (ap)T