a$)$

Write the simple linear regression equation for miles per gallon as the response variable and weight as the predictor variable. How might the car rental company use this model? See Step $4$ in the Python script.

b$)$

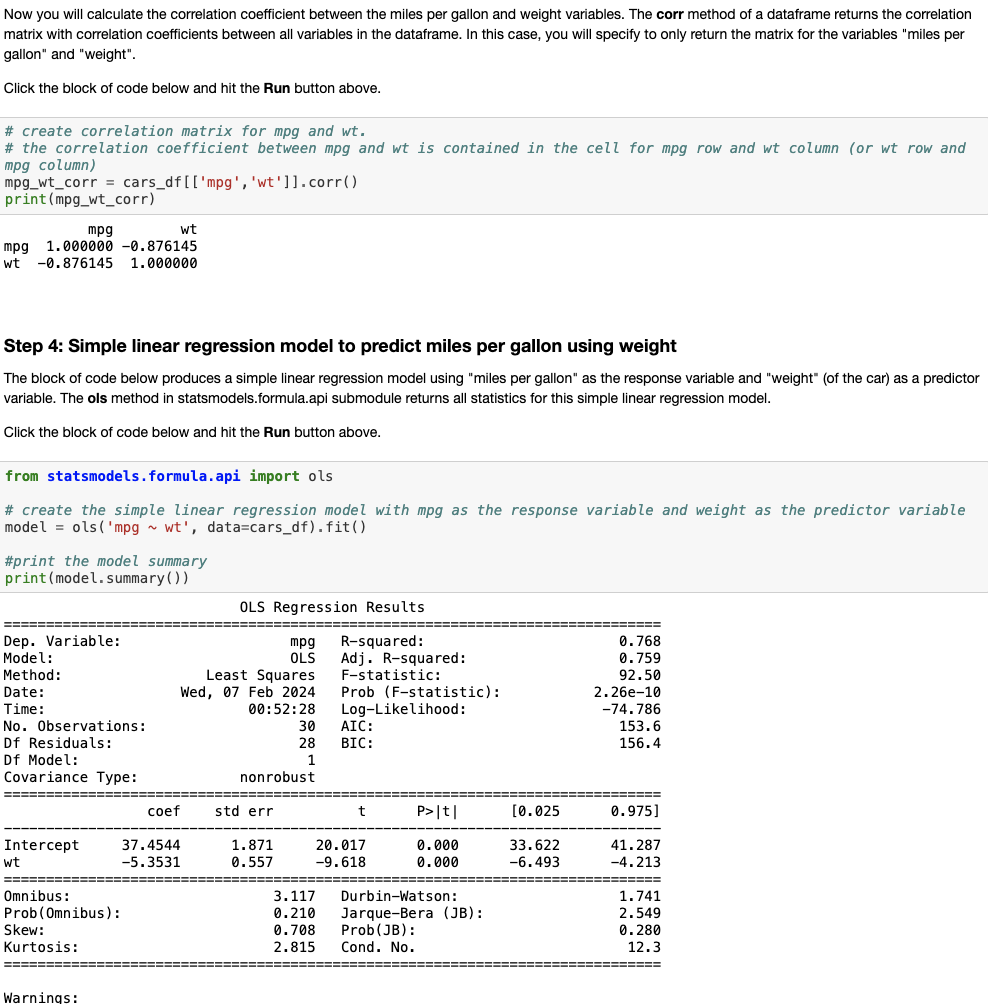
What is the slope coefficient? Is this coefficient significant at a $5\%$ level of significance $($alpha$=0\mathrm{.}05)?($Hint: Check the P$-$value, P is greater than the absolute valueNow you will calculate the correlation coefficient between the miles per gallon and weight variables. The corr method of a dataframe returns the correlation matrix with correlation coefficients between all variables in the dataframe. In this case, you will specify to only return the matrix for the variables "miles per gallon" and "weight".

Click the block of code below and hit the Run button above.

# create correlation matrix for mpg and wt$.$

# the correlation coefficient between mpg and wt is contained in the cell for mpg row and wt column $($or wt row and

mpg column$)$

mpg$\_$wt$\_$corr $=$ cars$\_$df $[[\text{'}$mpg$\text{'},\text{'}$wt$\text{'}]].$corr$()$

print$($mpg$\_$wt$\_$corr$)$

Step $4$: Simple linear regression model to predict miles per gallon using weight

The block of code below produces a simple linear regression model using "miles per gallon" as the response variable and "weight" $($of the car$)$ as a predictor variable. The ols method in statsmodels.formula.api submodule returns all statistics for this simple linear regression model.

Click the block of code below and hit the Run button above.

from statsmodels. formula.api import ols

# create the simple linear regression model with mpg as the response variable and weight as the predictor variable

model $=$ ols $(\text{'}$mpg $w{t}^{\text{'}},$ data$=$cars$\_$df$).$fit$()$

#print the model summary

print $($model$.$summary$())$

OLS Regression Results

$\backslash$table$[[$Dep$.$ Variable:,$mpg,$R$-$squared:,$0\mathrm{.}768],[$Model:$,$OLS,Adj. R$-$squared:,$0\mathrm{.}759],[$Method:$,$Least Squares,F$-$statistic:,$92\mathrm{.}50],[$Date:$,$Wed, $07$ Feb $2024,$Prob $($F$-$statistic$)$:$,2\mathrm{.}26e-10$ of t$,$ for weight in the Python output.$)$ See Step $4$ in the Python script.