Write the multiple regression equation for miles per gallon as the response variable. Use weight and horsepower as predictor variables. See Step 5 in the Python script. How might the car rental company use this model?

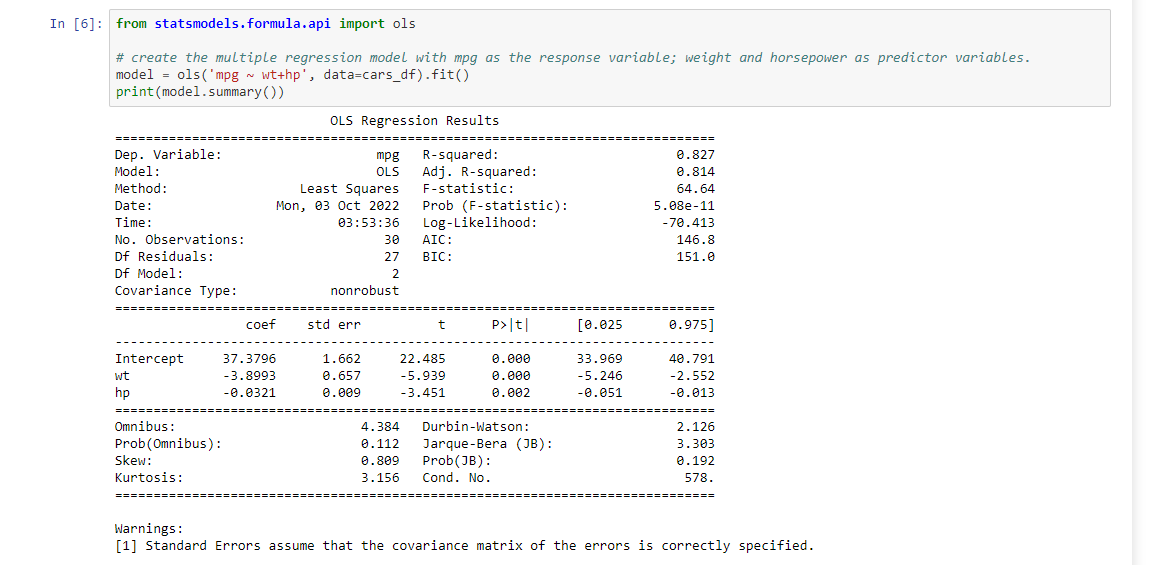
In [6]: from statsmodels. formula. api import ols # create the multiple regression model with mpg as the response variable; weight and horsepower as predictor variables. model = ols('mpg ~ wtthp', data=cars_df) . fit() print (model . summary ( ) ) OLS Regression Results Dep. Variable: mpg R- squared : 0.827 Model : OLS Adj. R-squared: 0. 814 Method : Least Squares F-statistic: 64.64 Date: Mon, 03 Oct 2022 Prob (F-statistic): 5. 08e-11 Time : 03:53:36 Log-Likelihood : -70. 413 No. Observations: 30 AIC : 146.8 Of Residuals: 27 BIC : 151.0 Df Model : 2 Covariance Type: nonrobust coef std err P> | t [0. 025 0.975] Intercept 37.3796 1. 662 22.485 0.060 33.969 40 . 791 wt -3.8993 0. 657 -5.939 0.000 -5.246 -2.552 hp -0. 0321 0.609 -3.451 0. 002 -0. 051 -0. 013 Omnibus : 4. 384 Durbin-Watson: 2.126 Prob (Omnibus ) : 0. 112 Jarque-Bera (JB) : 3.303 Skew : 0. 809 Prob(JB) : 0. 192 Kurtosis : 3.156 Cond. No. 578. == Warnings : [1] Standard Errors assume that the covariance matrix of the errors is correctly specified.Step 5: Multiple regression model to predict miles per gallon using weight and horsepower "his block of code produces a multiple regression model with "miles per gallon" as the response variable. and "ireight" and "horsepower" as predictor variables. "he ols method in statsmodelsrormulaapi suomodule returns all statistics for this multiple regression model. Click the block of code below and hit the Run button above