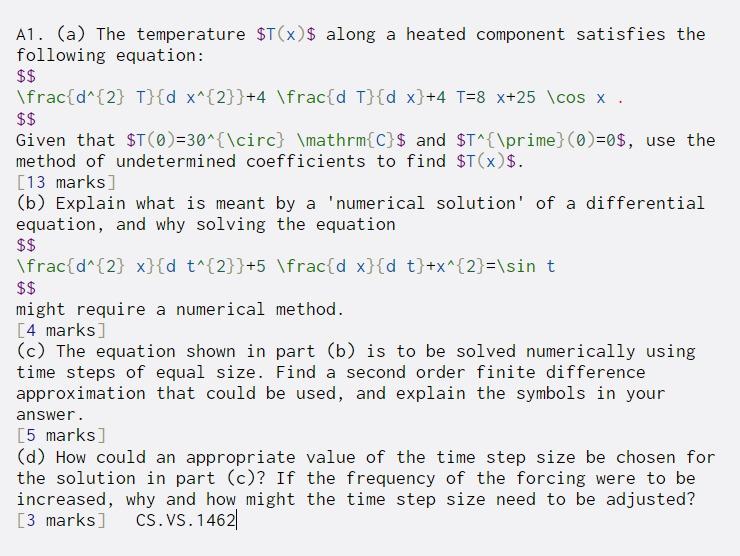
A1. (a) The temperature $T(x)$ along a heated component satisfies the following equation: $$ \frac{d^{2} T}{d x^{2}}+4 \frac{d T}{d x}+4 T=8 x+25 \cos x . $$ Given that $T()=30^{\circ} \mathrm{C}$ and $T^{\prime} ()=0$, use the method of undetermined coefficients to find $T(x)$. [13 marks] (b) Explain what is meant by a 'numerical solution' of a differential equation, and why solving the equation $$ \frac{d^{2} x}{d t^{2}}+5 \frac{d x}{d t}+x^{2}=\sin t $$ might require a numerical method. [4 marks] (c) The equation shown in part (b) is to be solved numerically using time steps of equal size. Find a second order finite difference approximation that could be used, and explain the symbols in your answer. [5 marks] (d) How could an appropriate value of the time step size be chosen for the solution in part (c)? If the frequency of the forcing were to be increased, why and how might the time step size need to be adjusted? [3 marks] CS.VS. 1462