Question: I have to find difference between ADI method on solving 2D diffusion equation with larger time-step and also 2D steady-state diffusion equation using centered difference

I have to find difference between ADI method on solving 2D diffusion equation with larger time-step and also 2D steady-state diffusion equation using centered difference method with smaller time-step. The boundary is Dirichlet.

Can anyone explain to me what the difference between this two?
here i attached the result i got from those methods. numerical and analytical solution for steady state diffusion (laplace) produce same answer without error.

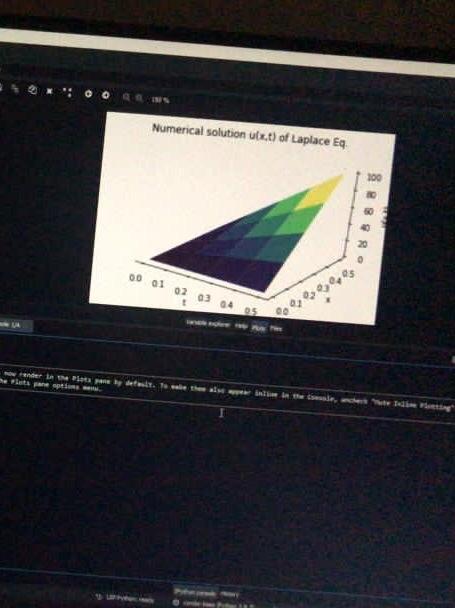
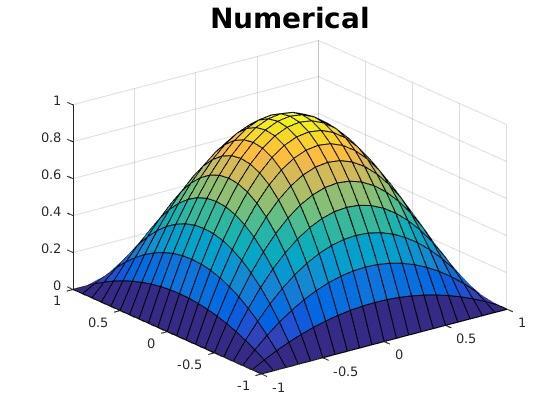
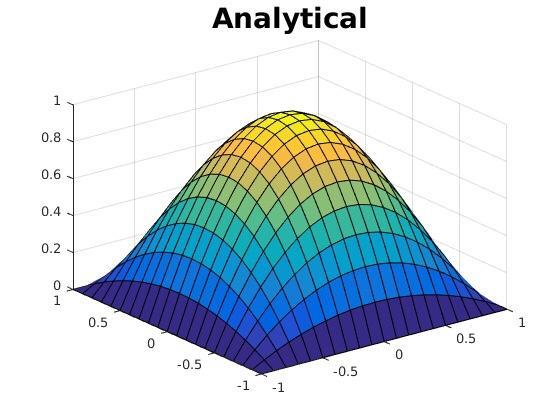
Numerical solution ulx.t) of Laplace Eq.3000102

Numerical110.870.60.470.2O0.510.50-0.5-0.5-1 -1

Analytical110.870.60.470.2O0.510.50-0.5-0.5-1 -1

Numerical solution ulx.t) of Laplace Eq 00 01 02 03 05 00 8 8 8 8 8 w render in the Pits pane by defasit. To ale thee alser inte in the sale, anche e di Pieting

Step by Step Solution

★★★★★

3.38 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

ADI method is an implicit method and centered difference method is an explicit method Because the AD... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Find how many muons reach detector B and C. The actual flux is energy dependent, decreasing with energy as ox E-27. For concrete- ness, the flux is 100 m s GeV (GeV) 27 for E> 1 GeV E where E is the...

If the residual interest of Grand Service Company is P180, 000 which is 2/3 of the total economic resources, what would be the amount of its economic obligation? a. P90, 000 b. P450, 000 c. P270, 000...

ADI apply the ADI method to the Dirichlet problem in Prob 5, using the grid in Fig. 455, as before and starting values zero.

A new startup has launched a line of organic skincare products that are free from harmful chemicals. The products are priced higher than other brands in the market but offer a superior quality. The...

Dawn Browne, an investment broker, has been approached by client Jack Thomas about the risk of his investments. Dawn has recently read several articles concerning the risk factors that can...

In describing the work of hedge funds, financial journalist Sebastian Mallaby has observed: [Research] showed that the unglamorous value stocks were underpriced relative to overhyped growth stocks....

APPLE T Changes of x on significance. The Statistical Significance applet illustrates statistical tests with a fixed level of significance for Normally distributed data with known standard deviation....

Accounting professionals must sometimes choose between two or more acceptable methods of accounting for business transactions and events. Explain why these situations can involve difficult matters of...

When we have a straight-line relation between two variables, we use a Pearson correlation coefficient. What does this coefficient describe?

5.86 Death penalty and false positives For the decision about whether to convict someone charged with murder and give the death penalty, consider the variables reality (defendant innocent, defendant...

Ethics Case Study 6: Is an AI system any different than a human doctor? What roles might trust or fear play? One way to think about algorithmic transparency in this case is to compare Charlie with a...

On July 5, 1852, Frederick Douglass said in his Fourth of July lecture at the Rochester NY Ladies Anti-Slavery Society meeting that the existence of enslavement in the United States "brands your...

Determine the highest real root of the given function using the following methods. f ( x ) = 2 . 1 x 3 - 1 1 . 6 x 2 1 7 . 5 x - 6 Use the secant method ( three iterations, x - 1 = 3 , x 0 = 4 ) and...

Use a weighted score model to choose between three methods (A, B, C) of financing the acquisition of a major competitor. The relative weights for each criterion are shown in the following table as...

What is a material amount from the perspective of auditors? Give an example of how that amount may differ based on the nature of the item.

State the principal assertions made by the auditors in the opinion paragraph of the AICPA auditors standard report.

Explain briefly the auditors responsibility for detecting noncompliance with laws by clients.

Contrast the roles of the AICPA and the PCAOB in the development of auditing standards.

In hypothesis testing, the common level of significance is a = 0.05. Some might argue for a level of significance greater than 0.05. Suppose that web designers tested the proportion of potential web...

Overview Change the code of lab 5 into a program with procedures. (If you have feedback comments or point deduction in lab 5, make sure to fix the code of lab 5 before starting lab 7. Don't get...

International Journal of Economics, Commerce and Management United Kingdom Vol. III, Issue 6, June 2015 http://ijecm.co.uk/ ISSN 2348 0386 MEASURING SERVICE QUALITY GAP IN HIGHER EDUCATION USING...

1. What is the paper about? 2. What are the five latent constructs that show different aspects of service quality? 3. What are the hypotheses of this paper? 4. How was sampling done for the study?...

Econometric: chapter 3: Multiple Regression Analysis Estimation could you do step by step? Problems 1 Using the data in GPA2 on 4,137 college students, the following equation was estimated by OLS:...

2: Difference, union and intersection operations (20 points) Table1 Table3 Table2 i, Find Difference TableD: Table1- Table2 ii. Find Union Tablel": Table1 U Table2 ill. Find Intersection "Tabke...

Create a class called ArrayUtility.java which will contain methods to perform array manipulations. There are no instance variables required in this class. Write each of the methods to solve each task...