Question: Ackerman's function is defined recursively on the nonnegative integers as follows: a(m, n) = n +1 a(m, n) = a(m-1, 1) a(m, n) = a(m-1,

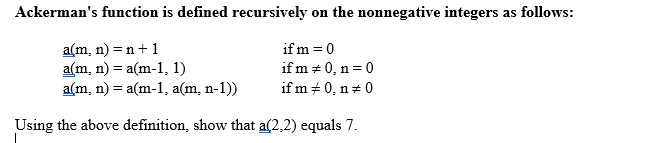
Ackerman's function is defined recursively on the nonnegative integers as follows:

Ackerman's function is defined recursively on the nonnegative integers as follows: a(m, n) = n +1 a(m, n) = a(m-1, 1) a(m, n) = a(m-1, a(m, n-1)) if m =0 if m=0, n=0 if m=0.n=0 Using the above definition, show that a(2.2) equals 7

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

I need the answer in Java. I need the circled area which is to devise a table lookup for the Ackermann function. I only need Java no other code. The secod picture shows what to expect from the lookup...

I want the code in java for the devise lookup method for Ackermann which is the 3rd question. It is said that we need two dimensional array to achive it. I have circled the part I want the code for....

In Java 1. Create a class Point with coordinate (x, y, z). Calculate the distance between two points p1 and p2 by using the class Point. (30 pts) 2. Write a method that accepts two arguments into the...

1- Assume the availability of a function called fact. The function receives an argument containing an integer value and returns an integer value. The function should return the factorial of the...

(Python 3.5, short and simple codes will suffice) 1. The sum of the numbers 1 to n can be calculated recursively as follows: The sum from 1 to 1 is 1. The sum from 1 to n is n more than the sum from...

Please write down the code in JAVA. Objectives .To gain experience with using recursion by implementing the Ackermann's Function. To gain experience with using class variables to record method...

NO1 and NO3 1Find /(1)/(2), / (3), and f (4) if f(n) is defined reur. 5. Determine whether each of these proposed definitions is a valid recursive definition of a function f from the set of...

Ackermanns function is defined recursively on non-negative integers as follows. A(m,n) = n+1 if m == 0 A(m,n) = A(m-1, 1) if m != 0, n == 0 A(m,n) = A(m-1, A(m, n-1)) if m != 0, n != 0 Implement it...

This is Discrete Math please help with Question 2 ke use of the definition of the object to define it. We define a basis step and a recursion step. what we are doing is different from mathematical...

Hi! I need to know why my answer to this Python problem about recursion and ADTs is not passing the tester. I will post the problem description, the tester, and my code. Unfortunately, indentation...

Beck was the general manager of Chilkoot Lumber Co. Haines sold fuel to the company. To persuade Haines to sell on credit, Beck signed a paper by which he promised to pay any debt the lumber company...

Which atom of each pair is larger? a. Si or S b. H or He

What is the purpose of the "Save More Tomorrow' program introduced by Thaler? To increase retirement savings over time Toincrease immediste spending To decrease overall savings To encourage long -...

The first scenario will be a Verbal Judo scenario in which your scenario follows the standard Verbal Judo interaction: You need to ask somebody to modify their behavior either to do something or to...

Identify legal considerations for different business communication purposes.

Discuss communication challenges in a global environment.

Describe key strategies for effective global business communication.