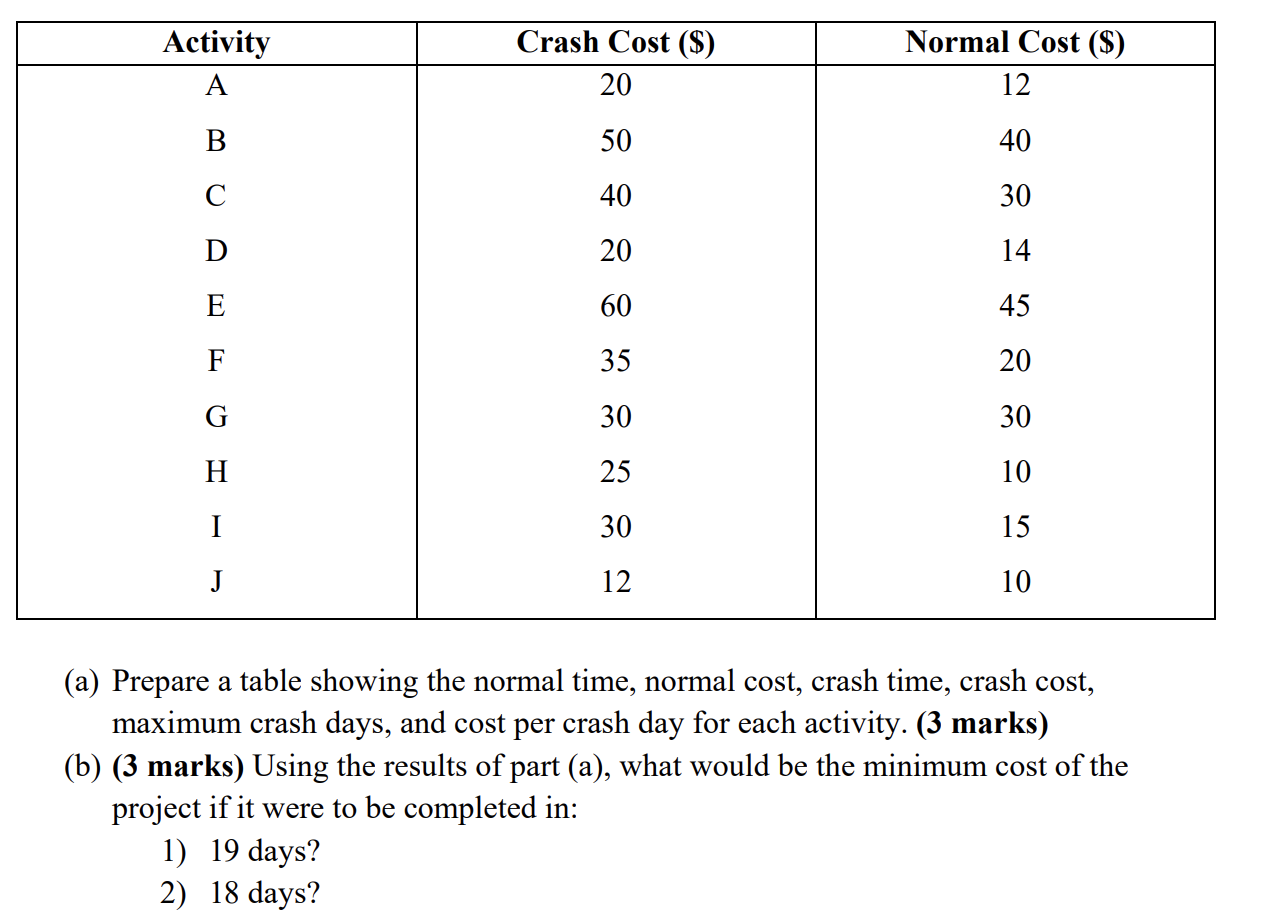
Activity A Crash Cost ($) 20 Normal Cost ($) 12 B 50 40 40 30 D 20 14 E 60 45 F 35 20 G 30 30 H 25 10 I 30 15 J 12 10 (a) Prepare a table showing the normal time, normal cost, crash time, crash cost, maximum crash days, and cost per crash day for each activity. (3 marks) (b) (3 marks) Using the results of part (a), what would be the minimum cost of the project if it were to be completed in: 1) 19 days? 2) 18 days? = = 3) 17 days? C) (4 marks) We want to formulate part of a linear programming (LP) model that will assess the additional cost of reducing the completion time to 9 days. Recall that the decision variables in the LP model are defined as: Xi = the finish time for activity i and Yi = the amount of time activity i is crashed, i = A, B, C, ..., J. Use the results of part (a) and the given precedence relationships among the activities of this project to answer the following questions: 1) State the objective function of the LP model. 2) Write the constraint(s) corresponding to the finish time of activity D. 3) Write the constraint(s) corresponding to the finish time of activity F. 4) Write the constraint(s) to ensure that the project will be completed in 9 days or less. Activity A Crash Cost ($) 20 Normal Cost ($) 12 B 50 40 40 30 D 20 14 E 60 45 F 35 20 G 30 30 H 25 10 I 30 15 J 12 10 (a) Prepare a table showing the normal time, normal cost, crash time, crash cost, maximum crash days, and cost per crash day for each activity. (3 marks) (b) (3 marks) Using the results of part (a), what would be the minimum cost of the project if it were to be completed in: 1) 19 days? 2) 18 days? = = 3) 17 days? C) (4 marks) We want to formulate part of a linear programming (LP) model that will assess the additional cost of reducing the completion time to 9 days. Recall that the decision variables in the LP model are defined as: Xi = the finish time for activity i and Yi = the amount of time activity i is crashed, i = A, B, C, ..., J. Use the results of part (a) and the given precedence relationships among the activities of this project to answer the following questions: 1) State the objective function of the LP model. 2) Write the constraint(s) corresponding to the finish time of activity D. 3) Write the constraint(s) corresponding to the finish time of activity F. 4) Write the constraint(s) to ensure that the project will be completed in 9 days or less