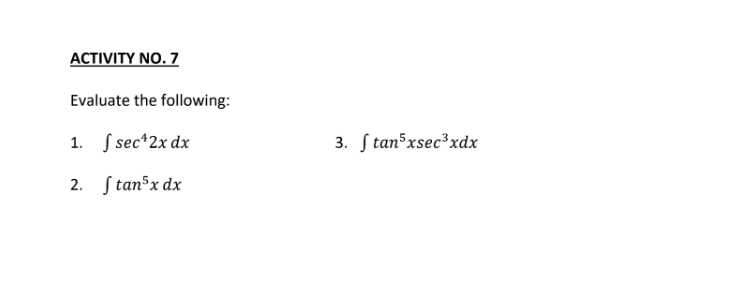
ACTIVITY NO. 7 Evaluate the following: 1. [ sec+2x dx 3. Stan xsecxdx 2. [ tan5x dxLESSON 9: TECHNIQUES OF INTEGRATION - POWERS OF TANGENTS and SECANTS IV. POWERS of TANGENTS and SECANTS Objectives: 1. Evaluate integrals involving powers of tangent and secant functions 2. Solve integration problems using previously learned trigonometric identities 3. Convert integrand into something that can be solved using previously discussed theorems 4. Make integration of complicated differentials easier General Form: Stanmusecrudx Where: v = function of x m, n = whole numbers Note: Do not interchange m and n; m is the exponent of the tangent function, n is the exponent of the secant function T49] Case 1. m is any number, n is an even integer greater than 2 [ tanmvsec"vax = [ tanmvsec"-2vsec2v dx Then use the identity sec20 = 1 + tan20 T50] Case 2. m is a positive odd integer, n is any number [ tan"vsec"vax = ] tanm-lvsec"-lvsec v tan vdx Then use the identity tan20 = sec20 - 1 T51] Case 3. m is positive, n is zero Stan"vax = S tanm-2vtan?vax Then use the identity tan20 = sec20 - 1