(a)Draw all possible full binary trees with 3 or fewer vertices.

(b)Draw all possible full binary trees with 5 vertices.

(c)Draw all possible full binary trees with 7 vertices.

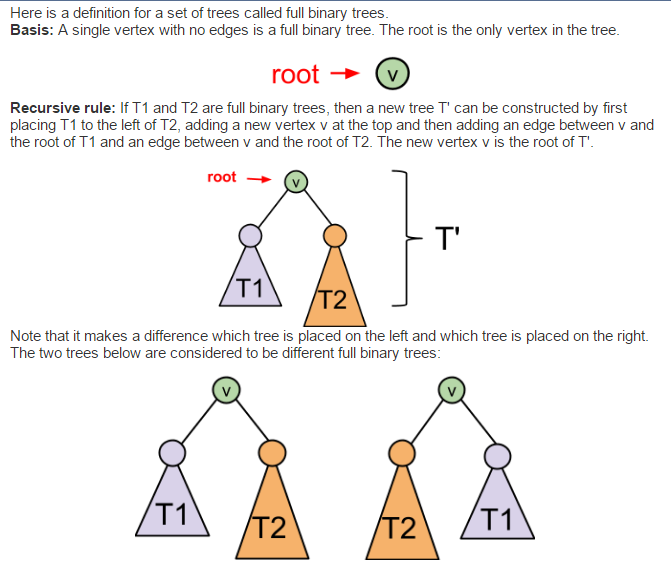
Here is a definition for a set of trees called full binary trees Basis: A single vertex with no edges is a full binary tree. The root is the only vertex in the tree root (v Recursive rule If T1 and T2 are full binary trees, then a new tree T can be constructed by first placing T1 to the left of T2, adding a new vertex v at the top and then adding an edge between v and the root of T1 and an edge between v and the root of T2. The new vertex v is the root of T root T' T1 Note that it makes a difference which tree is placed on the left and which tree is placed on the right The two trees below are considered to be different full binary trees