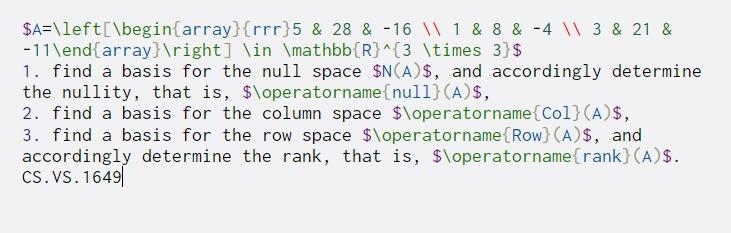
$A=\left(\begin{array}{rrr}5 & 28 & -16 \\ 1 & 8 & -4 3 & 21 & -11\end{array} ight] \in \mathbb{R}^{3 \times 3] $ 1. find a basis for the null space $N(A)$, and accordingly determine the nullity, that is, $\operatorname{null}(A)$, 2. find a basis for the column space $\operatorname{Col}(A)$, 3. find a basis for the row space $\operatorname{Row} (A)$, and accordingly determine the rank, that is, $\operatorname{rank}(A)$. CS.VS. 1649