ALGORITHMS DIRECTED GRAPH PROBLEM:

Given a directed graph G = (V, E) with capacity c(u, v) > 0 for each edge (u, v) E and demand r(v) at each vertex v V , a routing of flow is a function f such that

for all (u, v) E, 0 f(u, v) c(u, v), and

for all v V ,

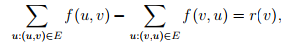
i.e., the total incoming flow minus the total outgoing flow at vertex v is equal to r(v). Notice that the demand r(v) can take positive value, negative value, or zero.

(a) Show how to find a routing or determine that one does not exist by reducing to a maximum flow problem.

(b) Suppose that additionally there is a lower bound l(u, v) > 0 at each edge (u, v), and we are looking for a routing f satisfying f(u, v) l(u, v) for all (u, v) E. Show how to find such a routing or determine that one does not exist by reducing to a maximum flow problem.

PLEASE SHOW ALL WORK STEPS. i AM TRYING TO UNDERSTAND HOW TO FIND THE SOLUTION TO THESE PROBLEMS

u:(u,v)EE u:(v,u)EE