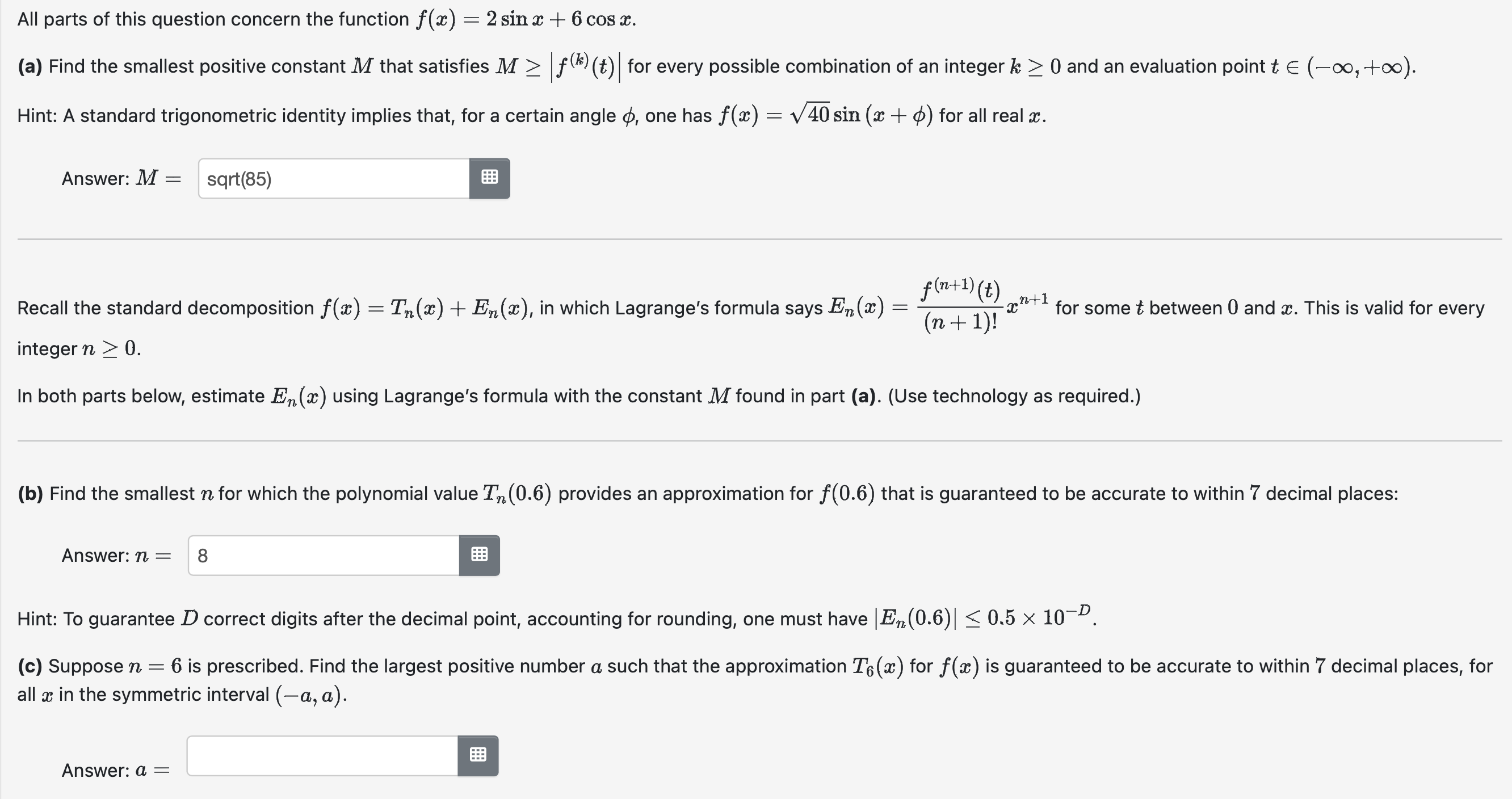
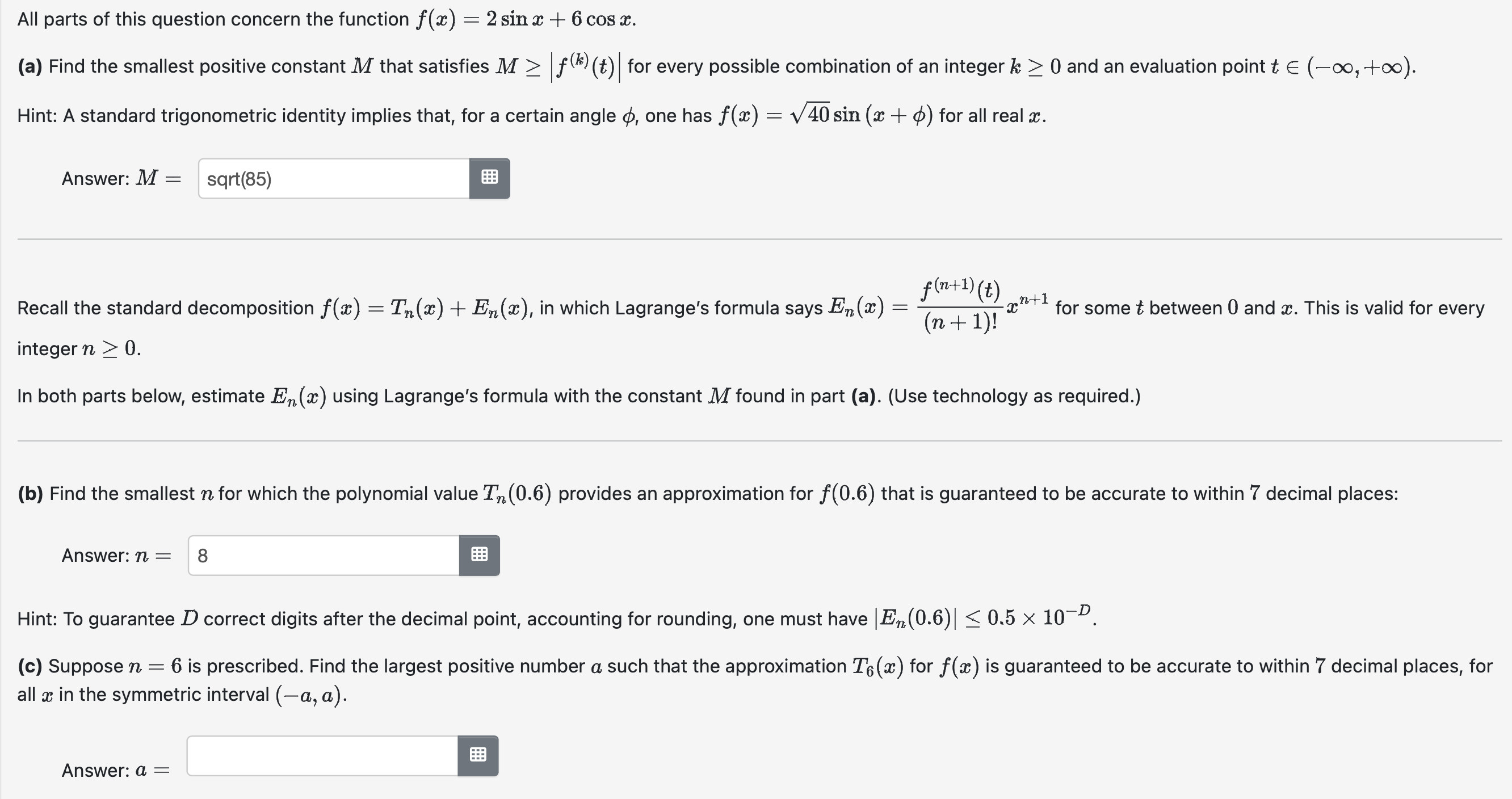
All parts of this question concern the function f(a:) = 2 sin a: + 6 cos :13. (3) Find the smallest positive constant M that satisfies M 2 'f(k)(t)' for every possible combination of an integer k: 2 0 and an evaluation pointt E (00, +00): Hint: A standard trigonometric identity implies that, for a certain angle ()5, one has f(:l:) = V40 sin (a: + 4)) for all real 2. Answer: M : sqrt(85) f(n+1) (t) n+1 (n+ 1)! m Recall the standard decomposition f(:z:) = Tn(:c) + En(:z;), in which Lagrange's formula says E7,(m) = for some t between 0 and 1:. This is valid for every integern 2 O. In both parts below, estimate E1500) using Lagrange's formula with the constant Mfound in part (3). (Use technology as required.) (b) Find the smallest nfor which the polynomial value Tn(0.6) provides an approximation for f(0.6) that is guaranteed to be accurate to within 7 decimal places: Answer: n = 8 Hint: To guarantee D correct digits after the decimal point, accounting for rounding, one must have lEn(0.6)| S 0.5 X 101). (c) Suppose n = 6 is prescribed. Find the largest positive number a such that the approximation T6(ar:) for at) is guaranteed to be accurate to within 7 decimal places, for all a: in the symmetric interval (0., a). Answer: a