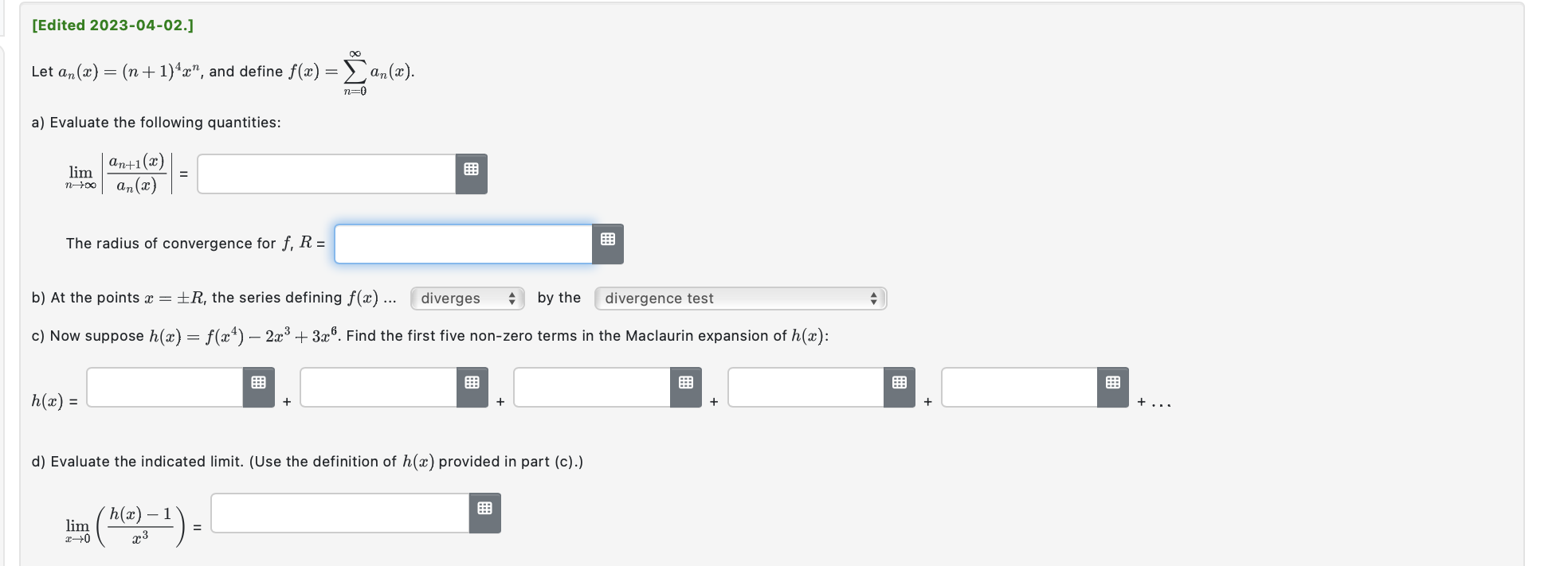
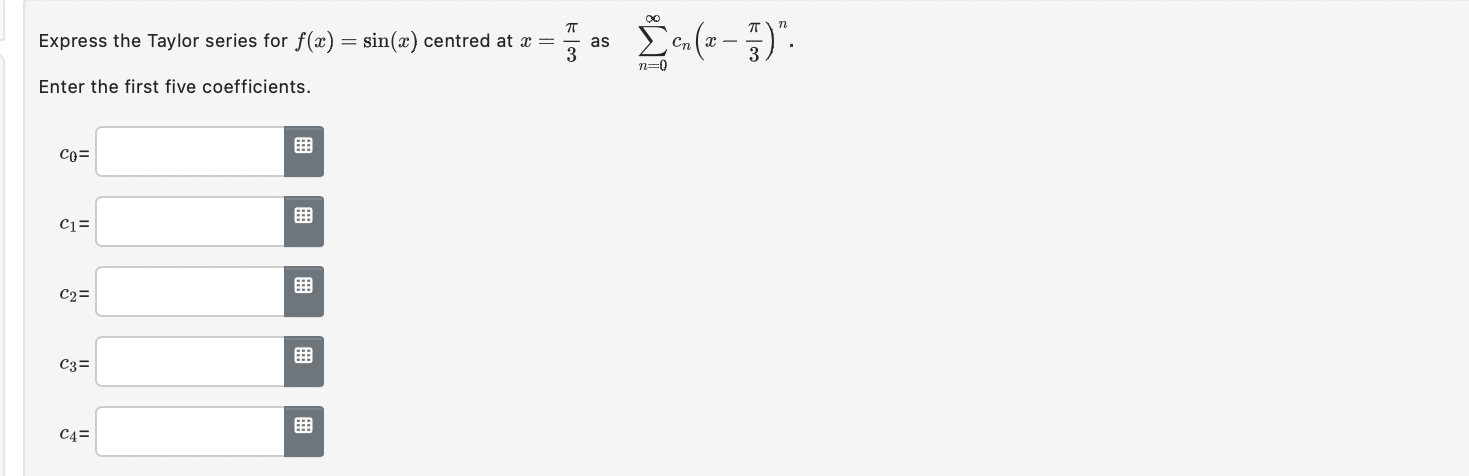
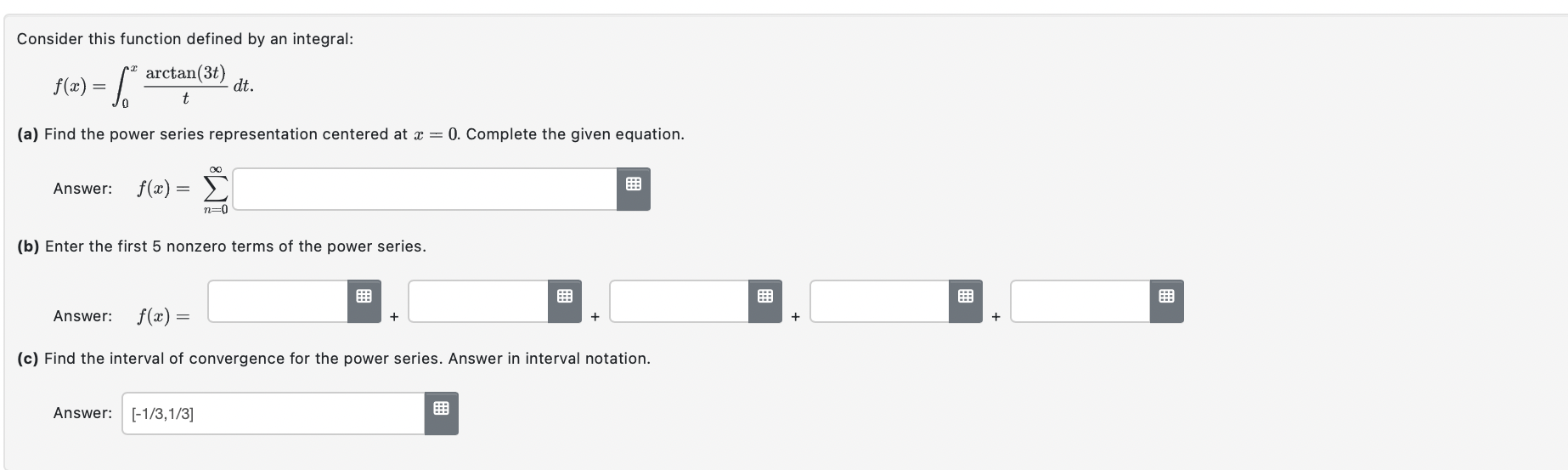
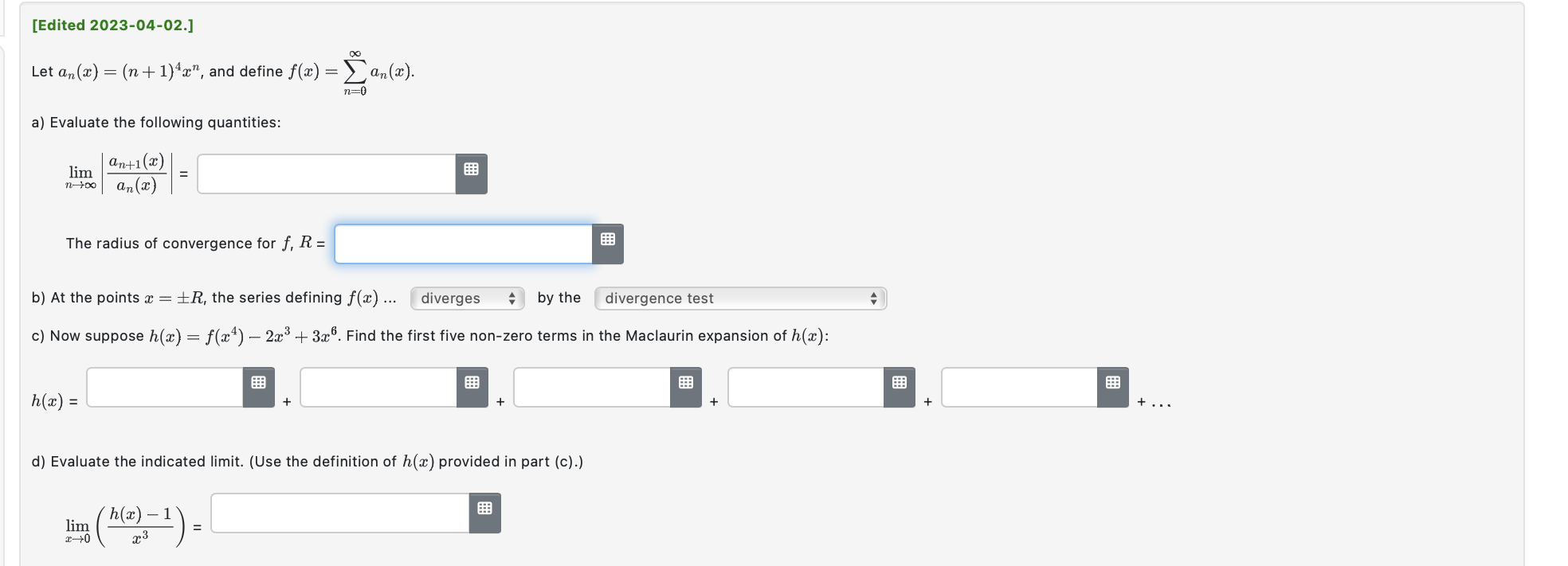
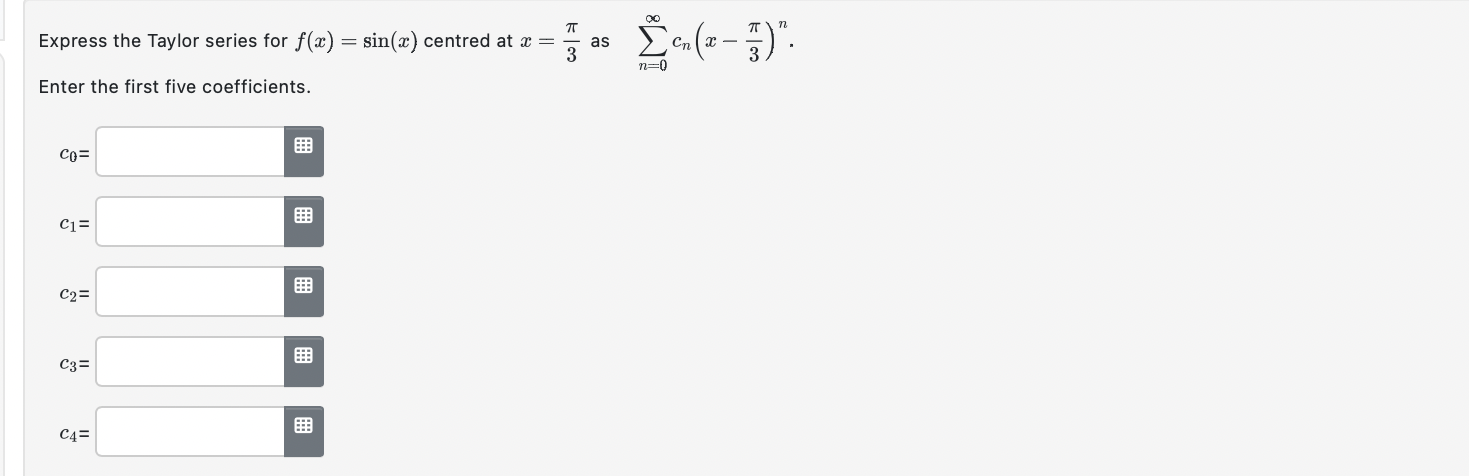
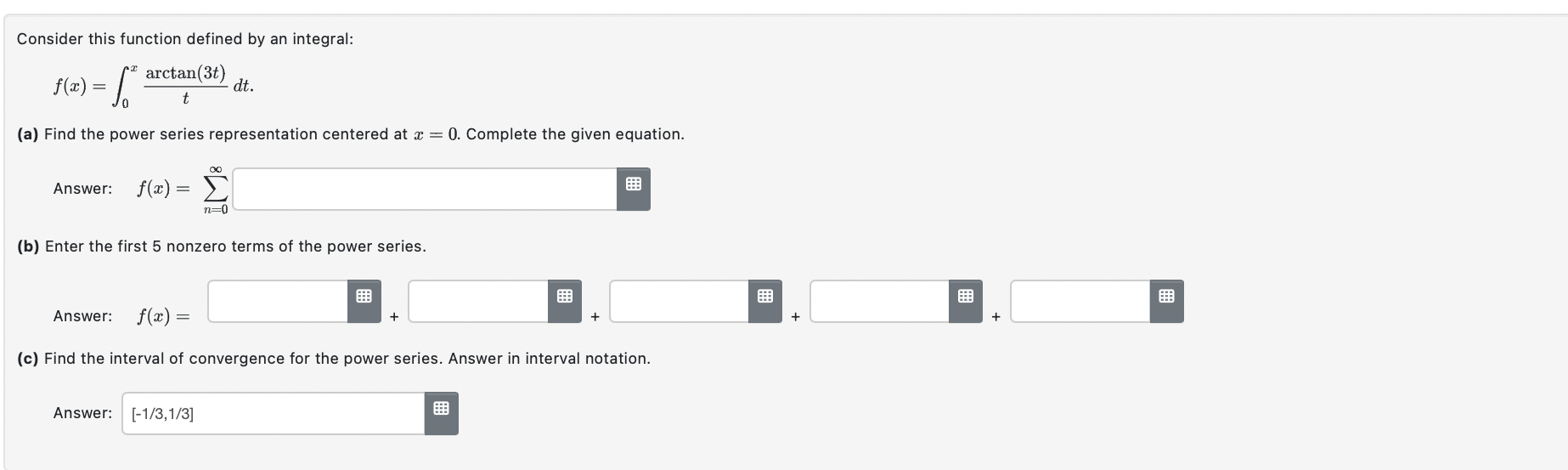
All parts of this question concern the function f(a:) : 551113: + 4 cos 1:. (a) Find the smallest positive constant M that satisfies M 2 lfw)' for every possible combination of an integer k 2 0 and an evaluation point t E (moo, +00). Hint: A standard trigonometric identity implies that, for a certain angle (:3, one has f(:c) : v 41 sin (a: + ) for all real ac. Answer: M: 1:!"th) {tn-H for some t between 0 and at. This is valid for every integer TL 2 U. ('n + 1.)! Recall the standard decomposition f(2) : Tn(1) + E42), in which Lagrange's formula says Emu) = In both parts below, estimate Em) using Lagrange's formula with the constant Mlound in part (a). (Use technology as required.) (b) Find the smallest n for which the polynomial value Tn(0.9) provides an approximation for f(0.9) that is guaranteed to be accurate to within 4 decimal places: Answer: n = Hint: To guarantee D correct digits after the decimal point, accounting for rounding, one must have |En(.9)l g 0.5 x 10'\". (6) Suppose n = 11 is prescribed. Find the largest positive number a such that the approximation Tn(:c) for f(:l') is guaranteed to be accurate to within 9 decimal places, for all m in the symmetric interval (emu). Answer: a = [Edited 2023-04-02.] Let an(x) = (n+ 1)4x", and define f(x) = >an(x). n=0 a) Evaluate the following quantities: lim anti (2) n-+Do an (2 ) The radius of convergence for f, R = b) At the points x = +R, the series defining f(x) ... diverges by the divergence test c) Now suppose h(x) = f(24) - 2x3+ 3x . Find the first five non-zero terms in the Maclaurin expansion of h(): h(x) = + + . .. d) Evaluate the indicated limit. (Use the definition of h(x) provided in part (c).) lim h(x) - 1 C-+0Express the Taylor series for f(x) = sin(x) centred at x = as [on ( 2 - # )". n=0 Enter the first five coefficients. CO= FEB C2= C3= C4=Find the first six coefficients for which the following identity holds on some nonempty open interval including 3 = 0: Answers: Co: Cg: (33: C4: 0:: Hyatze4h = E cum\". \":0 Consider this function defined by an integral: f(a:) =1: arctan(3t) dt. 15 (3) Find the power series representation centered at x = 0. Complete the given equation. on Answer: f(r)= 2 n=0 (h) Enter the first 5 nonzero terms of the power series: Answer: f(9:) : (c) Find the interval of convergence for the power series. Answer in interval notation. Answer: [~1/3,1/3] . Find the exact sums of the series given below. A. 144924;):(;)4+...+(;)"+.._= 53 55 57 1"5"'\"+1 a. 5++--+( ) 3: 5! 7! (2n+1)1+'": Hint: These are point-values of the power series for certain familiar functions