all the bubbles please fill! if possible do it on the image

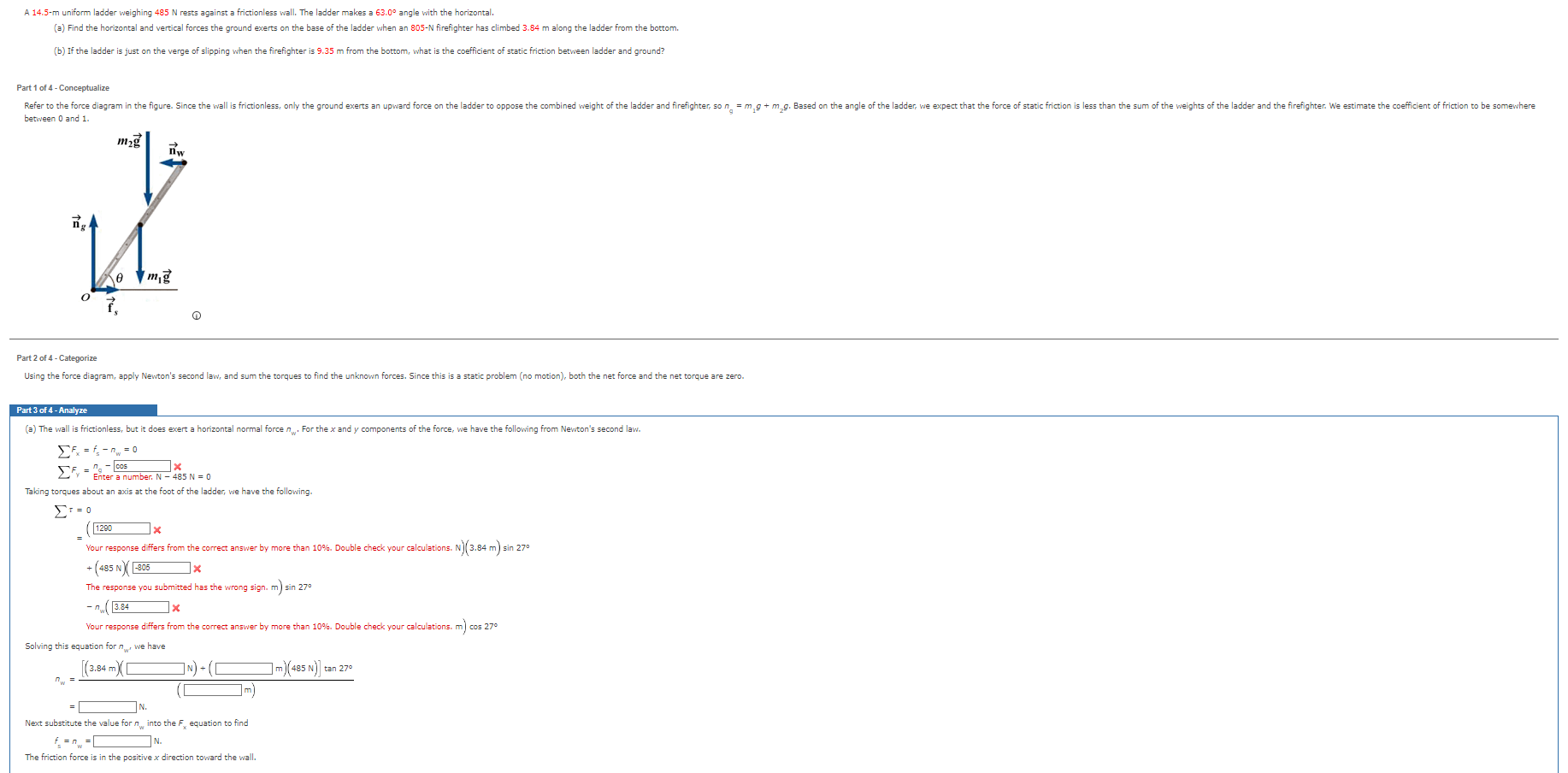
A 14.5-m uniform ladder weighing 485 N rests against a frictionless wall. The ladder makes a 63.0% angle with the horizontal. (a) Find the horizontal and vertical forces the ground exerts on the base of the ladder when an 805-N firefighter has climbed 3.84 m along the ladder from the bottom. (b) If the ladder is just on the verge of slipping when the firefighter is 9.35 m from the bottom, what is the coefficient of static friction between ladder and ground? Part 1 of 4 - Conceptualize Refer to the force diagram in the figure. Since the wall is frictionless, only the ground exerts an upward force on the ladder to oppose the combined weight of the ladder and firefighter, son, = m, g + m,g. Based on the angle of the ladder, we expect that the force of static friction is less than the sum of the weights of the ladder and the firefighter. We estimate the coefficient of friction to be somewhere between 0 and 1. n2g nw Vmig Part 2 of 4 - Categorize Using the force diagram, apply Newton's second law, and sum the torques to find the unknown forces. Since this is a static problem (no motion), both the net force and the net torque are zero. Part 3 of 4 - Analyze (a) The wall is frictionless, but it does exert a horizontal normal force ,. For the x and y components of the force, we have the following from Newton's second law. EF = - nw =0 CFv = Enter a number. N - 485 N = 0 Taking torques about an axis at the foot of the ladder, we have the following. 1290 1 x Your response differs from the correct answer by more than 109%. Double check your calculations. N)(3.84 m) sin 279 + (485 N) -805 1x The response you submitted has the wrong sign. m) sin 27% - 1 3.84 Your response differs from the correct answer by more than 109%. Double check your calculations. m) cos 27 Solving this equation for nw. we have (3.84 m)( 7N) + m) (485 NV)] tan 270m) N. Next substitute the value for n, into the F, equation to find f =nw =[ N. The friction force is in the positive x direction toward the wall