Alter the code below to create a program that includes k1 and k2, using Euler's improved two-step method, and reduces the error by a factor of four instead of two.

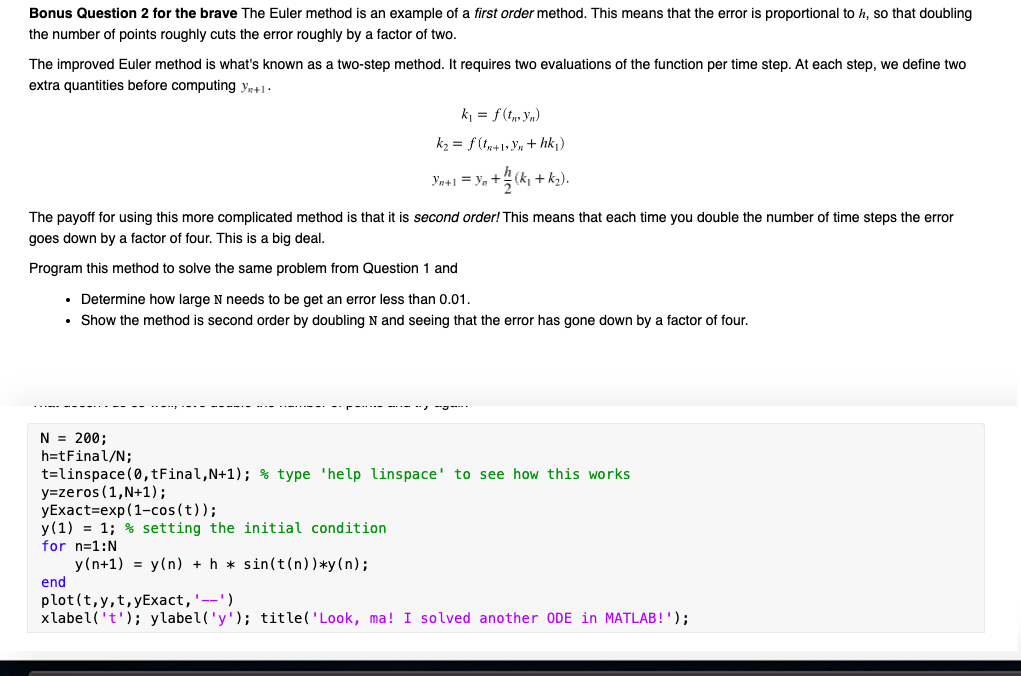
Bonus Question 2 for the brave The Euler method is an example of a first order method. This means that the error is proportional to h, so that doubling the number of points roughly cuts the error roughly by a factor of two. The improved Euler method is what's known as a two-step method. It requires two evaluations of the function per time step. At each step, we define two extra quantities before computing yet. k = f (ty) kz = f (tx+1 Yx + hk) Yn+1 = y + (ki + ky). The payoff for using this more complicated method is that it is second order! This means that each time you double the number of time steps the error goes down by a factor of four. This is a big deal. Program this method to solve the same problem from Question 1 and Determine how large N needs to be get an error less than 0.01. Show the method is second order by doubling N and seeing that the error has gone down by a factor of four. ---... -- -- --- ---- ---- - --- ..-..- . N = 200; h=tFinal/N; t=linspace(0,tFinal,N+1); % type 'help linspace' to see how this works y=zeros (1,N+1); yExact=exp(1-cos(t)); y(1) = 1; % setting the initial condition for n=1:N y(n+1) = y(n) + h * sin(t(n))*y(n); end plot(t,y,t,yExact,'--') xlabel('t'); ylabel('y'); title('Look, ma! I solved another ODE in MATLAB!')