Using matlab

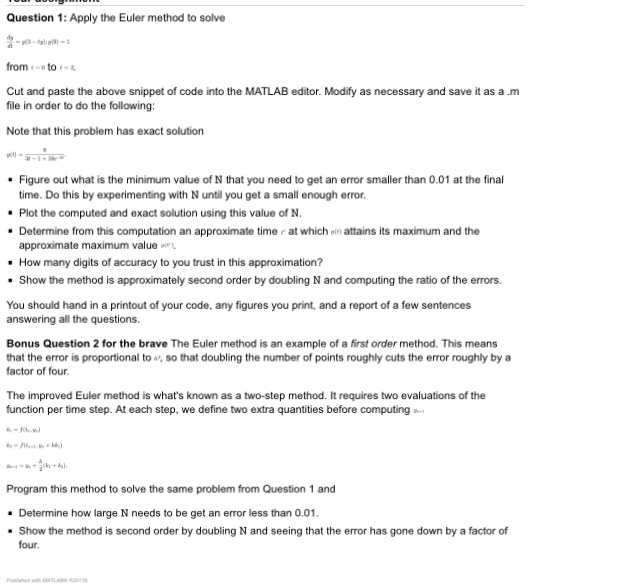
Question 1: Apply the Euler method to solve from-to- Cut and paste the above snippet of code into the MATLAB editor. Modify as necessary and save it as a m file in order to do the following Note that this problem has exact solution Figure out what is the minimum value of N that you need to get an error smaller than 0.01 at the final time. Do this by experimenting with N until you get a small enough error. Plot the computed and exact solution using this value of N Determine from this computation an approximate time r at which vin attains its maximum and the approximate maximum value How many digits of accuracy to you trust in this approximation? . Show the method is approximately second order by doubling N and computing the ratio of the errors. You should hand in a printout of your code, any figures you print, and a report of a few sentences answering all the questions. Bonus Question 2 for the brave The Euler method is an example of a first order method. This means that the error is proportional to so that doubling the number of points roughly cuts the error roughly by a factor of four The improved Euler method is what's known as a two-step method. It requires two evaluations of the function per time step. At each step, we define two extra quantities before computing Program this method to solve the same problem from Question 1 and - Determine how large N needs to be get an error less than 0.01 Show the method is second order by doubling N and seeing that the error has gone down by a factor of four